ElGamal加密解密以及签名密码体系

最近有好多晚自习，好喜欢，有好多时间学密码，哈哈哈哈哈哈（已疯

上代码

签名部分原理依据：密码学——elgama加解密及数字签名算法_elgamal签名算法-CSDN博客

应用

"""
Do you kown the ElGamal?
One day, Alice want to contect with Bob by ElGamal,so she used this system made by saga131
This time ,you are Bob.
Next time ,maybe you are a hacker to attack this system.
"""

from Crypto.Util.number import *
from gmpy2 import *
from random import randint


class MyElGamal:
    def __init__(self, bit):
        self.p = getPrime(bit)
        self.g = randint(1, self.p-1)
        self.x = randint(1, self.p-1)
        self.y = pow(self.g, self.x, self.p)
        # 下面是用于签名的参数
        while True:
            self.k = randint(1, self.p-1)
            if gcd(self.k, self.p-1) == 1:
                break
        self.r = pow(self.g, self.k, self.p)

    def getPrivateKey(self):
        return self.x

    def getPublicKey(self):
        return self.y, self.g, self.p

    def encrypt(self, m):
        if type(m) is not int:
            m = bytes_to_long(m)
        while True:
            entropy = randint(1, self.p-1)
            if gcd(entropy,self.p-1) == 1:
                break

        c1 = pow(self.g, entropy, self.p)
        c2 = pow(self.y, entropy, self.p)*m % self.p
        c = (c1, c2)
        return c

    def decrypt(self, c, x=None):
        if x is None:
            x = self.x
        c1 = c[0]
        c2 = c[1]
        c1x = pow(c1, x, self.p)
        m = c2*inverse(c1x, self.p) % self.p
        return long_to_bytes(m)

    # 生成签名
    def getDigitalSignature(self, plaintext):
        import hashlib
        if type(plaintext) is not bytes:
            plaintext = plaintext.encode("utf-8")
        hashed_plaintext = hashlib.sha256(plaintext).hexdigest().encode()
        hm = bytes_to_long(hashed_plaintext)
        s = (hm-self.x*self.r)*inverse(self.k, self.p-1)
        return self.r, s

    # 签名验证
    @staticmethod
    def toVerify(plaintext, y, g, p, r, s):
        import hashlib
        if type(plaintext) is not bytes:
            plaintext = plaintext.encode("utf-8")
        hashed_plaintext = hashlib.sha256(plaintext).hexdigest().encode()
        hm = bytes_to_long(hashed_plaintext)
        g1 = pow(y, r, p)*pow(r, s, p)
        g2 = pow(g, hm, p)
        return g1 == g2


Alice = MyElGamal(1024)
Bob = MyElGamal(1024)


message = b"flag{******}"
ds = Alice.getDigitalSignature(message)
hex_ds = []
for i in ds:
    hex_ds.append(hex(i))

send_message = str((message,hex_ds)).encode("utf-8")
# 签名太长了，只好将信息分组发送
block = [send_message[i:i+128] for i in range(0, len(send_message), 128)]
# print(block)
# print(bytes_to_long(send_message).bit_length())
c = []
for i in block:
    c.append(Bob.encrypt(i))


print("Alice通过不太安全的渠道发过来的密文：", c)
print("Alice通过Wechat发过来的公钥：", Alice.getPublicKey())
print("你通过Wechat发过去的公钥：", Bob.getPublicKey())
print("你作为Bob肯定知道自己的私钥为：", Bob.getPrivateKey())

"""
Alice通过不太安全的渠道发过来的密文： [(5559204086144384871799930748464942869370842710505680224125898144643793973465414481353626828046695064758916241494331110137135547428432564583729655427198539575171387164567177557747112837071019362452505293748475319261664442936198006771007371265970322396723075769994353783953462442541429036606486427600672475671, 67201230465292159598999218353173095011875787969801785689608716453256293800596465863809960279860674268623257450386038240119985611432468895210816481803921883663625967344025365828457899746652150368470653315673806528964738406912111070836459953514546019507832765340980300739582771276679689623917028880588301401538), (113138083874195244824641523191760868385587980192310309015470873889440879804185975056168710372922987478332123822141407279524322670653219043775071286618665920492650376384949119718424837838796621843128087815803366383594270667097661381720939703686050479328889156673499973328141963310996966817418729968244901761278, 52063633010806598185978024789239474992613451360387784071378954836606061790280773100194961518797682669962299551219540415218873990738657522945473476299700872770956663655428002485814280198399866562659722941049777669434469210847813146750179047650586433641652763579029030262575346464673222588784131173578299133189), (18284045190551283332182858660486635328831687676222655957179745932442532233059541437011129716344114730818508841643972982169253438018744109837003355397640676827071984906389846884171522749071455659022988971941811290666598666857238455823992956971189946322108491192051155688808124579449960230271889123633298326016, 87234149463314125743228551421474520423332935882830757306245391734278011253751676053584195956083944489572770500648083283645356725484721083514745240054427292659870970584250615232300186386936999748857374322429768466906289162059137431573486134494234336307442959233121292602742532426586270508660342076678257600891), (101415933602050294435061950518997872441245753122794421430918600659800124340221392425415882432790970154796929524831091721546951241441644252990232850339138683614392404922818147805442160215916801059711805644996296333714323925771983868983514668583984646069918555594611639336110874391897474481686827816639511927255, 109431026397419594693733269791709835368925937341949561393174428815194794132333389296719291456845146092178853999741357425723555755456295993150506525380847125646415205983235257039787018673634872712834129140828259288905956737264391681626601450742034703495417893674379434705160273745062810369953334395116223172722), (56590731621617649179335296873804186742864645336978589802680415813339663124886218311718918988816318945584621943292154737267558972825835804054680462040051614667024806503414836776873349205690928926279651518895633229003477312908315851813159987426194341270447458375894948078300942791574331327271814553979695166078, 99187579467003162798209496472532950952723574638710643702009157062812226725598311998874014028454110223251404617772924242802858479360933976927071811974824613481282281513093545226152469698308837437844134185378044116379248233612127398655680031654404478141043437190065695086755950402468604961396541954674509844733), (94324201026806591769326426794482723397453235272931172061418011428905596127320792104362414812979496154853110685661005593284236018225461809175591996578894254325600238909928133801605617273098929748587757749348894121791648422509206607103630006823085813450066191945340979402624066612552431700637040432877571620265, 64382914321008928922558465596804659429688781978877832951140603779812187215637632200663164880109822470147621333186118613110991640102026995130117203605486435468844798465834756700564277861266123988388709026826359921619487726690184946041353695549031961174045495288129252573305634341901459113219825424110082366932), (6125310408594054920154366917562922466083052283341449908215292886752787400037981772300734230956300305344719711560681727629846325627524065097301050115273290643278620853507080602337114949092980324086439600942473771173336788584612569020118092602218489660493710846372356657521451202351857098707180548506315185500, 28381402308661853145923964495608488995690750396828898422710260566346301791954824014762394309935656049889316808410371062428153965690330223820196039799626885001910108699406920635626150718934101899285511017356244401525867976057005359972360213132897743399506628673082290270239189978135623640834271256230564381655), (15645437557908034926273768567321443404700760235002199163002281149950809011883787867639704638354681630023804971478679307418428145798187082168233659635902340363691429434389037941983862866438193283197381683804786056280506346689604385301461838514307780225401812148521468264476409907044197807938545664633291589138, 83167840344830303393417333041543371580257915322973407323242387269366338118044476878803248277624882247028944216618777294995545389921511834916566797311569455223956132098170556107301685443321752696899951651385876370519853119451457540948998295851963909074277752085383222923108168214426254608282892716575617928423), (93863239267824672905791683955358348074666199679856286629819837240596333051601911755853532480926499747992596818733038264260579738950681303806000505488505850269621183412715373121200623362297630128249747635666296325043053846784911473750447805314864564357360102860273922317792129568975863791140743354692096498858, 57914648209347881437047635428350174787453298859532200752762192337138405228261765262193768649056550271440780935635325628195240022822209300934628647306037219165736160953194681580358825721299594564859013681355372141095646160438486226660781605256638684231732479565918737725446751225394197430932784378276174985368)]
Alice通过Wechat发过来的公钥： (99912548433963014155143269907465712209294575260654674208540056107046939294785141464768664790423593008567592004473348581402153210783996592950589580426867144588135245163469377000400168959197076662201143612250540017935675112002027620326786764012109342270731426851945288882815708522286703206188101676449471607577, 120366155020089608501015337344821518813479814904610833709789795611710014029207691912459817262313530077800081167327442302107408894302335055802191505745703828640788824144226147716299903431332805193418333939317945243257102696507294519309754505297845137703355982539995934706472230747016150142856681599971682681699, 164491671504266972810540181220621764494035224990993867619761254613497915826691059446738092911093644560267256535633297554683486602340850853022680420705481023626008073830274823428765428578793146799007825373096874965681541288495892683290055180285448096420133555947071055441369084642008455173401167529509987447481)
你通过Wechat发过去的公钥： (80929978552058410373276743728381283781187781795846295926046073983629680082006133104330358163928118662903102831400360003456238397367541528652184159932349719745859041692296789568100634355234371620795577008180980298067673004120834280448692257281451555425790580467278609886470514416089953157240475918832197326008, 77955537869512614389645867269435229557094306154345654989005302664256776742018595753747240028934945122147755205452169532408491197173796258212383827261786353489155977169450692703422289822703941665687518540181221490377302622615638685350596305446545546394880807767963492311294550697837824246745964322820950367110, 117567947116157749604071091013109250042213035401345433472989668571431226630192204149979385014679360718859179490698246385906759523814129966153943170733908885199986717728470424302104431252174319993561980561210038004796134364456991364204378953137276529031814327156440301008673104582519815462007610272000725494787)
你作为Bob肯定知道自己的私钥为： 69298133066764454193251494222924760265703880146246062810217039891927179674115611508526889650808209534992758501744204100315648535878881840144631830839140556149911814608281028231187851044082974214019292018965045357689491631844206968167056605939914533291783912350637466031428762453101705783311438770580866026549"""

EXP

from Crypto.Util.number import *
from gmpy2 import *
from random import randint

class MyElGamal:
    def __init__(self, bit):
        self.p = getPrime(bit)
        self.g = randint(1, self.p-1)
        self.x = randint(1, self.p-1)
        self.y = pow(self.g, self.x, self.p)
        # 下面是用于签名的参数
        self.k = randint(1, self.p-1)
        self.r = pow(self.g, self.k, self.p)

    def getPrivateKey(self):
        return self.x

    def getPublicKey(self):
        return self.y, self.g, self.p

    def encrypt(self, m):
        if type(m) is not int:
            m = bytes_to_long(m)
        while True:
            k = randint(1, self.p-1)
            if gcd(k,self.p-1) == 1:
                break

        c1 = pow(self.g, k, self.p) % self.p
        c2 = pow(self.y, k, self.p)*m % self.p
        c = (c1, c2)
        return c

    def decrypt(self, c, x=None):
        if x is None:
            x = self.x
        c1 = c[0]
        c2 = c[1]
        c1x = pow(c1, x, self.p)
        m = c2*inverse(c1x, self.p)
        return long_to_bytes(m).decode()

    # 生成签名
    def getDigitalSignature(self, plaintext):
        import hashlib
        if type(plaintext) is not bytes:
            plaintext = plaintext.encode("utf-8")
        hashed_plaintext = hashlib.sha256(plaintext).hexdigest().encode()
        hm = bytes_to_long(hashed_plaintext)
        s = (hm-self.x*self.r)*inverse(self.k, self.p-1)
        return self.r, s

    # 签名验证
    @staticmethod
    def toVerify(plaintext, y, g, p, r, s):
        import hashlib
        if type(plaintext) is not bytes:
            plaintext = plaintext.encode("utf-8")
        hashed_plaintext = hashlib.sha256(plaintext).hexdigest().encode()
        hm = bytes_to_long(hashed_plaintext)
        g1 = pow(y, r, p)*pow(r, s, p)
        g2 = pow(g, hm, p)
        return g1 == g2

c = [(5559204086144384871799930748464942869370842710505680224125898144643793973465414481353626828046695064758916241494331110137135547428432564583729655427198539575171387164567177557747112837071019362452505293748475319261664442936198006771007371265970322396723075769994353783953462442541429036606486427600672475671, 67201230465292159598999218353173095011875787969801785689608716453256293800596465863809960279860674268623257450386038240119985611432468895210816481803921883663625967344025365828457899746652150368470653315673806528964738406912111070836459953514546019507832765340980300739582771276679689623917028880588301401538), (113138083874195244824641523191760868385587980192310309015470873889440879804185975056168710372922987478332123822141407279524322670653219043775071286618665920492650376384949119718424837838796621843128087815803366383594270667097661381720939703686050479328889156673499973328141963310996966817418729968244901761278, 52063633010806598185978024789239474992613451360387784071378954836606061790280773100194961518797682669962299551219540415218873990738657522945473476299700872770956663655428002485814280198399866562659722941049777669434469210847813146750179047650586433641652763579029030262575346464673222588784131173578299133189), (18284045190551283332182858660486635328831687676222655957179745932442532233059541437011129716344114730818508841643972982169253438018744109837003355397640676827071984906389846884171522749071455659022988971941811290666598666857238455823992956971189946322108491192051155688808124579449960230271889123633298326016, 87234149463314125743228551421474520423332935882830757306245391734278011253751676053584195956083944489572770500648083283645356725484721083514745240054427292659870970584250615232300186386936999748857374322429768466906289162059137431573486134494234336307442959233121292602742532426586270508660342076678257600891), (101415933602050294435061950518997872441245753122794421430918600659800124340221392425415882432790970154796929524831091721546951241441644252990232850339138683614392404922818147805442160215916801059711805644996296333714323925771983868983514668583984646069918555594611639336110874391897474481686827816639511927255, 109431026397419594693733269791709835368925937341949561393174428815194794132333389296719291456845146092178853999741357425723555755456295993150506525380847125646415205983235257039787018673634872712834129140828259288905956737264391681626601450742034703495417893674379434705160273745062810369953334395116223172722), (56590731621617649179335296873804186742864645336978589802680415813339663124886218311718918988816318945584621943292154737267558972825835804054680462040051614667024806503414836776873349205690928926279651518895633229003477312908315851813159987426194341270447458375894948078300942791574331327271814553979695166078, 99187579467003162798209496472532950952723574638710643702009157062812226725598311998874014028454110223251404617772924242802858479360933976927071811974824613481282281513093545226152469698308837437844134185378044116379248233612127398655680031654404478141043437190065695086755950402468604961396541954674509844733), (94324201026806591769326426794482723397453235272931172061418011428905596127320792104362414812979496154853110685661005593284236018225461809175591996578894254325600238909928133801605617273098929748587757749348894121791648422509206607103630006823085813450066191945340979402624066612552431700637040432877571620265, 64382914321008928922558465596804659429688781978877832951140603779812187215637632200663164880109822470147621333186118613110991640102026995130117203605486435468844798465834756700564277861266123988388709026826359921619487726690184946041353695549031961174045495288129252573305634341901459113219825424110082366932), (6125310408594054920154366917562922466083052283341449908215292886752787400037981772300734230956300305344719711560681727629846325627524065097301050115273290643278620853507080602337114949092980324086439600942473771173336788584612569020118092602218489660493710846372356657521451202351857098707180548506315185500, 28381402308661853145923964495608488995690750396828898422710260566346301791954824014762394309935656049889316808410371062428153965690330223820196039799626885001910108699406920635626150718934101899285511017356244401525867976057005359972360213132897743399506628673082290270239189978135623640834271256230564381655), (15645437557908034926273768567321443404700760235002199163002281149950809011883787867639704638354681630023804971478679307418428145798187082168233659635902340363691429434389037941983862866438193283197381683804786056280506346689604385301461838514307780225401812148521468264476409907044197807938545664633291589138, 83167840344830303393417333041543371580257915322973407323242387269366338118044476878803248277624882247028944216618777294995545389921511834916566797311569455223956132098170556107301685443321752696899951651385876370519853119451457540948998295851963909074277752085383222923108168214426254608282892716575617928423), (93863239267824672905791683955358348074666199679856286629819837240596333051601911755853532480926499747992596818733038264260579738950681303806000505488505850269621183412715373121200623362297630128249747635666296325043053846784911473750447805314864564357360102860273922317792129568975863791140743354692096498858, 57914648209347881437047635428350174787453298859532200752762192337138405228261765262193768649056550271440780935635325628195240022822209300934628647306037219165736160953194681580358825721299594564859013681355372141095646160438486226660781605256638684231732479565918737725446751225394197430932784378276174985368)]
Alice_pk = (99912548433963014155143269907465712209294575260654674208540056107046939294785141464768664790423593008567592004473348581402153210783996592950589580426867144588135245163469377000400168959197076662201143612250540017935675112002027620326786764012109342270731426851945288882815708522286703206188101676449471607577, 120366155020089608501015337344821518813479814904610833709789795611710014029207691912459817262313530077800081167327442302107408894302335055802191505745703828640788824144226147716299903431332805193418333939317945243257102696507294519309754505297845137703355982539995934706472230747016150142856681599971682681699, 164491671504266972810540181220621764494035224990993867619761254613497915826691059446738092911093644560267256535633297554683486602340850853022680420705481023626008073830274823428765428578793146799007825373096874965681541288495892683290055180285448096420133555947071055441369084642008455173401167529509987447481)
Bob_pk = (80929978552058410373276743728381283781187781795846295926046073983629680082006133104330358163928118662903102831400360003456238397367541528652184159932349719745859041692296789568100634355234371620795577008180980298067673004120834280448692257281451555425790580467278609886470514416089953157240475918832197326008, 77955537869512614389645867269435229557094306154345654989005302664256776742018595753747240028934945122147755205452169532408491197173796258212383827261786353489155977169450692703422289822703941665687518540181221490377302622615638685350596305446545546394880807767963492311294550697837824246745964322820950367110, 117567947116157749604071091013109250042213035401345433472989668571431226630192204149979385014679360718859179490698246385906759523814129966153943170733908885199986717728470424302104431252174319993561980561210038004796134364456991364204378953137276529031814327156440301008673104582519815462007610272000725494787)
Bob_sk = 69298133066764454193251494222924760265703880146246062810217039891927179674115611508526889650808209534992758501744204100315648535878881840144631830839140556149911814608281028231187851044082974214019292018965045357689491631844206968167056605939914533291783912350637466031428762453101705783311438770580866026549

def decrypt(c, x, p):

    c1 = c[0]
    c2 = c[1]
    c1x = pow(c1, x, p)
    m = c2 * inverse(c1x, p) % p
    return long_to_bytes(m)

m = []
for i in c:
    m.append(decrypt(i, Bob_sk, Bob_pk[2]))

print(m)

plaintext = b"".join(m)
print(plaintext)

def toVerify(plaintext, y, g, p, r, s):
    import hashlib
    if type(plaintext) is not bytes:
        plaintext = plaintext.encode("utf-8")
    hashed_plaintext = hashlib.sha256(plaintext).hexdigest().encode()
    hm = bytes_to_long(hashed_plaintext)
    g1 = pow(y, r, p) * pow(r, s, p) % p
    g2 = pow(g, hm, p)
    return g1 == g2

r = 0x9c3f0d5fa8b6846ee525a113d76cfe9cf6be4b824d9b3574989a2a1ada3acaa263b50c3b8f0494408b16c2c14d34edfb3e1f184d04ebafca273f5251826c7fff6f22512a78c567af2022f6c872bbf8ed9eaaa9a0f79a9ba4bde1a92d7432f68960079959404b91f631d291599f8df88e05f7a5caf9c0566da24a2c5a485870ac
s = -0x1595f857d5e2e501426d11fe2914b092668faa572ae36ae117de24b1d36a77200018b87f9f6e49485c8cde289a8ad69ae51539247cd2d092d1a4d0d34b56cb2e174183c0d6b042e39c58cc01dbf50dc8ff8c918ee8272a6692a16e6bed1e70b2b1acfbf1d8d1adac75f53e450d25034d9aad0b1c86f06eb206be7a8a74b5fa4707d4517f3f4fcf420d621f4bdb301726028e80a24129513e33adc72f39a1b8845a6e480a53b66e7b13bf83d9df418a89e9e641c648536a2d8bd72ecfd5c5119fff1ab1ddf59bba8391a91f206de0b634f2d8df163c0353c043f5af4a56c053a0e24acebaec285542dabb13c4d2c6645bd4e6158ba087467c580ae0f4c4a192b11f2a467a21495d4c6f4e179d1f949f468a27b4e7d82ab151c7efd7df38fff0e593e53e4da36fbe21069528622f22e693a5e31b57eb67e599867cb990d15c04372764641e13292abcd2958f87e122061c322ad5f2ba2a104030af9c19f766035ffda9419adf40b738c054332a4f3647cf78cecc421b41a437fac0a1b2cfe3e2bb
m = b'flag{Change_your_mindset_and_view_things_calmly}'
print(toVerify(m, Alice_pk[0],Alice_pk[1],Alice_pk[2],r, s))  # 留意这里要用谁的公钥
# True

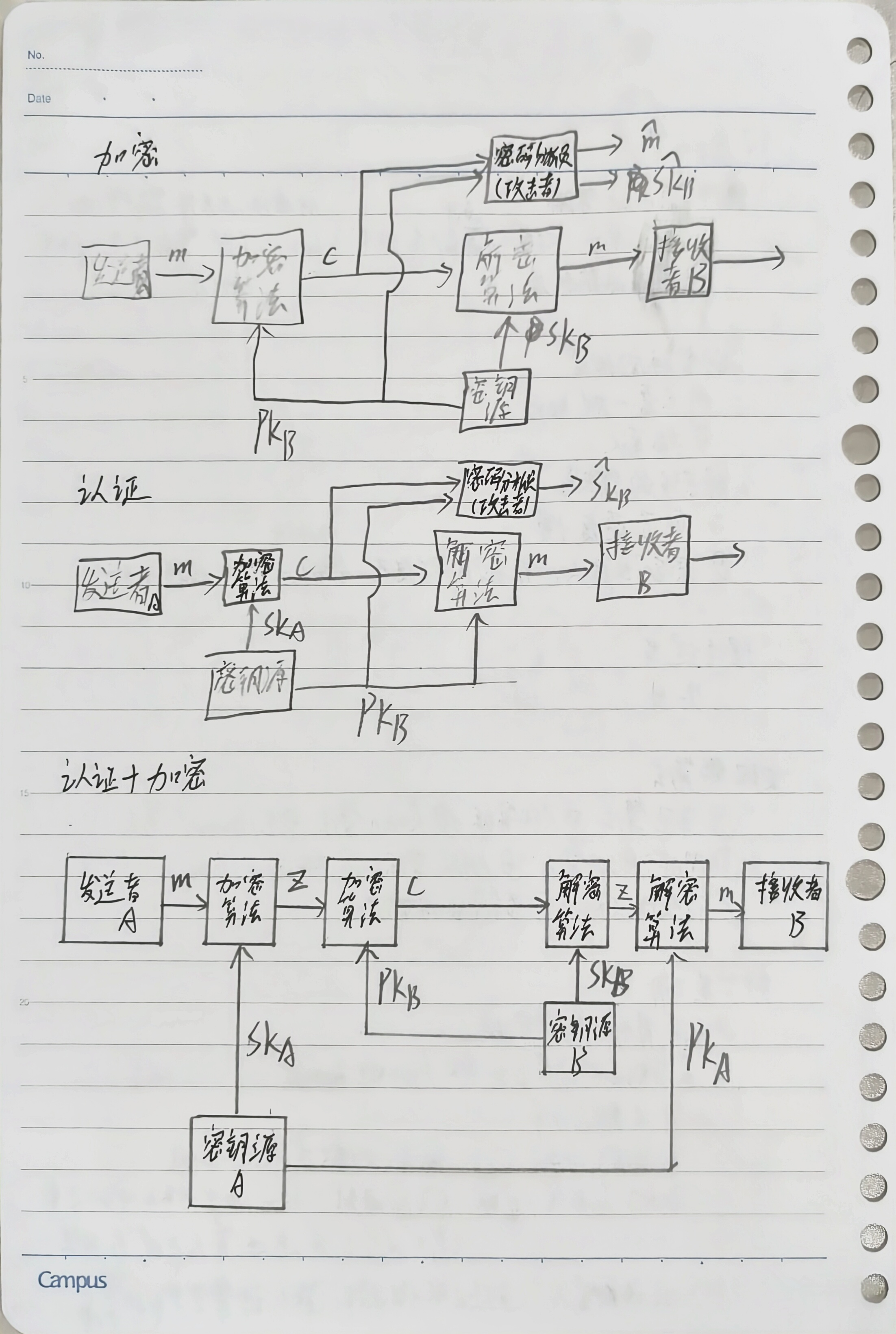
敲代码的思路图

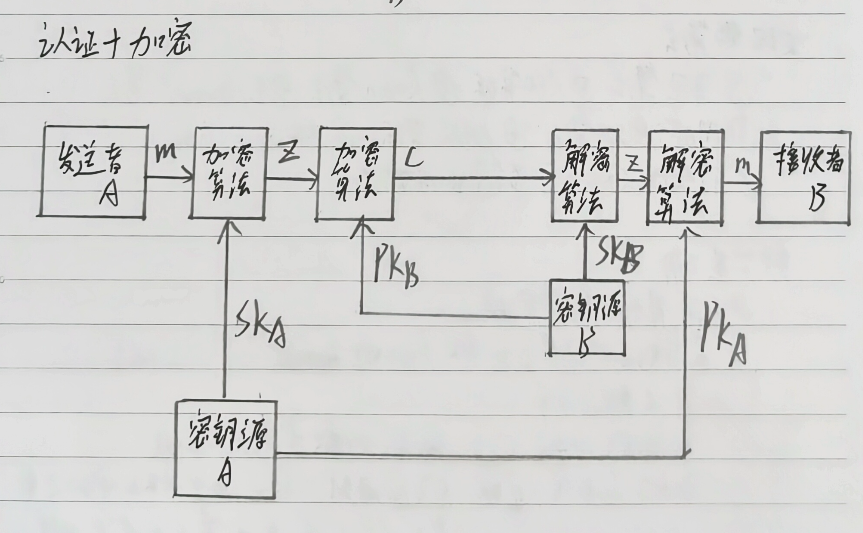
ElGamal密码算法

部分参考：密码学——elgama加解密及数字签名算法_elgamal签名算法-CSDN博客

参数

• p：大素数
• g,x：两个小于p的随机数
• y: $y = g^x \mod p$
• （y，g，p）作为公钥，x是私钥
• k：临时密钥，小于p，并且与p-1互质的随机数
• entropy：小于p，且与p-1互质的随机数，用于签名
• r: $r = g^{entropy} \mod p$，用于签名

加密

$$\begin{align}c_1 &= g^{k} \mod p\\ c_2 &= y^{k} \times m\mod p \end{align}$$

C = (c1, c2)

解密

$$m = \frac{c_2}{c_1^x}\\ \frac{c_2}{c_1^x}\equiv \frac{y^{k} \times m}{g^{x\times k }} \equiv \frac{y^{k} \times m}{y^{k}}\equiv m \mod p$$

并没有什么原理，只是关系式而已

数字签名

回顾一下参数

• entropy：小于p，且与p-1互质的随机数，用于签名
• r: $r = g^{entropy} \mod p$，用于签名

如果我k和entropy相等会怎么样

生成

计算m的哈希值，获得hm

$$s = \frac{hm-x\cdot r}{k} \pmod {p-1}$$

签名为（r，s）

签名验证

计算接收到明文（具体要不要包含签名视情况而定，即看代码）的哈希值$hm’$

计算由签名得出的g1（包含对方私钥确认信息$x$）

$$g_1 = y^r\cdot r^s\mod p$$

由接收得到的明文计算g2

$$g_2 = g^{hm} \mod p$$

比较g1与g2是否相等

原理

$$g_1 \equiv y^r\cdot r^s \equiv g^{x\cdot r}\cdot g^{k\cdot s}\equiv g^{x\cdot r+k\cdot \frac{hm-x\cdot r}{k}} \equiv g^{hm} \mod p$$

没有数学原理，都是套关系。

分组

经过实验，p为1024位时，每次可加密128字节的明文，所以分组的代码为

block = [send_message[i:i+128] for i in range(0, len(send_message), 128)]