Polarctf——RSA1-2逐步解析

2025-03-25

字数统计: 1.2k字 | 阅读时长≈ 5分

感觉有趣，便记录下来，应该会逐步更新，先写一个getflag2先（3月27已更新完），后续考虑录一个视频讲解，但也是后话。

getflag2

题目代码块

def getflag2(m):
    result = []
    for i in range(2):
        result.append(getPrime(bits))
    p, q = result
    n = p * q
    hint1 = pow(m, p, n)
    hint2 = pow(m, q, n)
    print('---------- getflag 2 ----------')
    print(f'{hint1 = }')
    print(f'{hint2 = }')
    print(f'{n = }')

官方给出的WP

分析

首先说一下用到的数学原理——费马小定理或者欧拉定理，以及中国剩余定理的思路。

已知

$hint1\equiv m^{p}\mod n……①\\ hint2 \equiv m^{q}\mod n……②\\ n,e,c具体值$

接下来我们分析一下由哪些地方可以让我们获得到p或者q（rsa大部分解法）

先入为主的肯定是m头上那诱惑的p，导致主播想用离散对数来求解，冷静下来的主播想起p的位数是512位，此方案不通。
其次是模数中的n，可以降为$k\cdot p$ (具体原因如下$^{[1]}$)，而且给出了两个式子，可以尝试寻找之间的联系，我们从这里入手。

由①式得

$\begin{align*} hint1 &= m^{p} + k\cdot n ~~~~\#将n分解,并两边同时模上p\\ &\equiv m^{p} + k\cdot p\cdot q\mod p\\ &\equiv m\mod p\\ &=m + k\cdot p \end{align*}$

怎么让这个结果与②式有联系呢，我们观察①②差别，幂不同，一个是p，一个是q，那么n可以联系两个式子。

$\begin{align*} hint1^{n} &\equiv m^{p\cdot p\cdot q} \mod p ~~~\#由模的性质可以得出\\ &\equiv ((m^{p}~~\% p~)^p~~~\% p ~)^q \mod p \end{align*}$

而$m^{p}~~\% p = m$，套两层p，得出的结果也是m

得出

$\begin{align*} hint1^{n}&\equiv m^q \mod p\\ &=m^q +k\cdot p \end{align*}$

此时，怎么解出p已经不言而喻了。

$\begin{align*} hint1^{n}&=m^q +k_1\cdot p……③\\ hint2 &\equiv m^{q} +k_2\cdot p……④ \end{align*}$

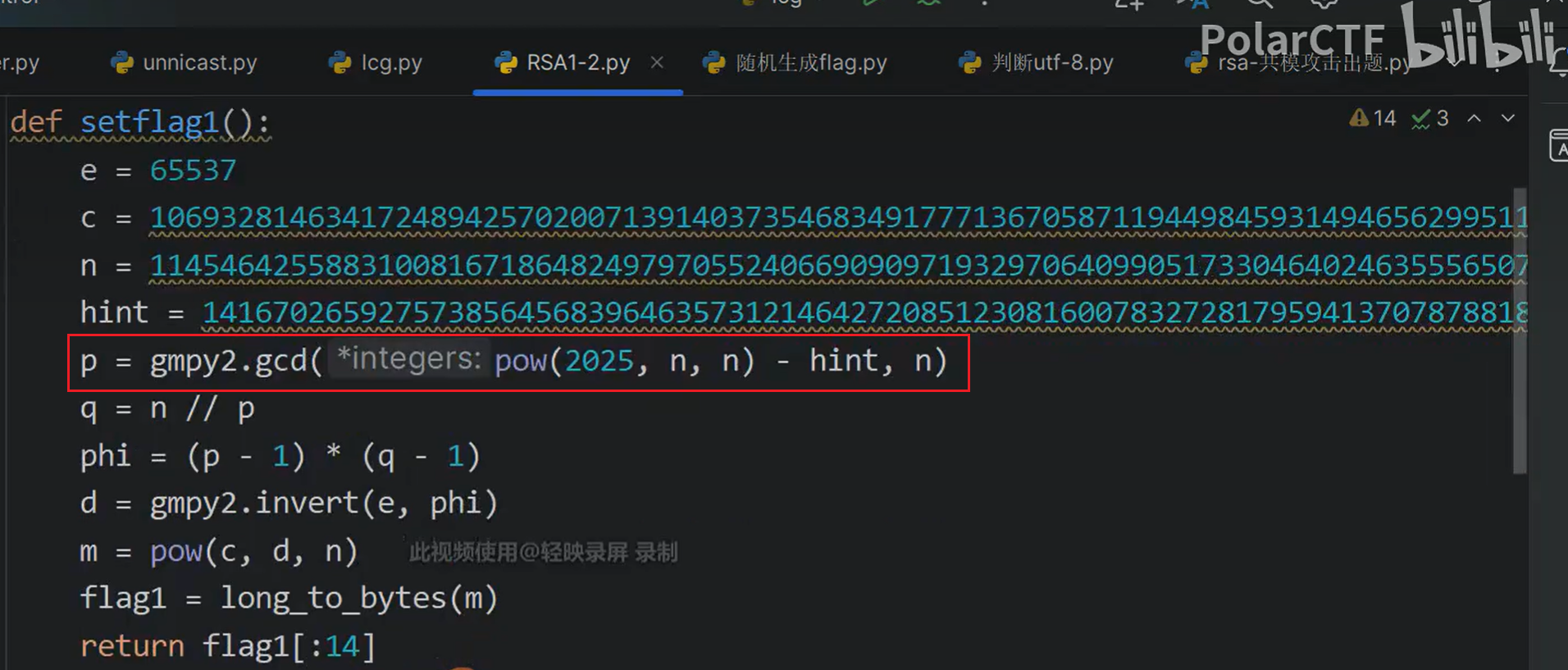
③-④得$k\cdot p$，与n求最大公因数，即可得到p。

getflag1

题目代码块

def getflag1(m):
    result = []
    for i in range(2):
        result.append(getPrime(bits))
    p, q = result
    if p <= q:
        p, q = q, p
    e = 0x10001
    n = p * q
    c = pow(m, e, n)
    hint = pow(2024 * p + 2025, q, n)
    print('---------- getflag 1 ----------')
    print(f'{c = }')
    print(f'{n = }')
    print(f'{hint = }')

官方解法

分析

已有

$hint \equiv (2024\cdot p+2025)^q \mod n\\ n,e,c具体值$

见到括号，先拆括号

$hint = C_q^0\cdot(2024\cdot p)^q+C_q^1\cdot(2024\cdot p)^{q-1}\cdot 2025+......+C_q^{q-1}\cdot (2024\cdot p)^1\cdot 2025^{q-1}+C_q^q\cdot 2025^q+k\cdot p\cdot q$

观察一下，我们可以从哪里获取到p或者q

多项式系数中含有q
$2024\cdot p$
2025的幂q
$k\cdot p\cdot q$中

多项式系数：注意最后倒数第二项，会生成一个n出来，$2024\cdot n\cdot 2025^{q-1}$，但这个对这题没有帮助

$2024\cdot p$太多了。

2025降幂太大了。

这个式子太多p了，让我们简化一下，将单个p提取出来，得到

$hint = 2025^q +k\cdot p ……①$

也可以理解成先取模p，然后再展开

$\begin{align} hint &\equiv 2025^q \mod p\\ hint &= 2025^q+k\cdot p \end{align}$

那么我们现在要剔除$2025^q$，用费马小定理构造一个

$\begin{align} 2025^n&\equiv 2025^{p\cdot q} \mod n\\ \#将模数降为p\\ 2025^n&\equiv 2025^{p\cdot q} \mod p\\ &\equiv (2025^p ~~~\%p)^q \mod p ~~~~~\#费马小定理\\ &\equiv2025^q \mod p \end{align}$

即$2025^n=2025^q+k\cdot p$

整体是在n下运行的，那么我们再模上n来加快计算速度

最终我们运用的算式为

$2025^n\equiv2025^q+k\cdot p \mod n ……②$

综上

$hint = 2025^q +k\cdot p ……①\\ 2025^n\equiv2025^q+k\cdot p \mod n ……②$

①-②得

$\begin{align} hint-2025^n&\equiv (k_1-k_2)\cdot p \mod n\\ &=(k_1-k_2)\cdot p + k_3\cdot p\cdot q\\ &=K\cdot p \end{align}$

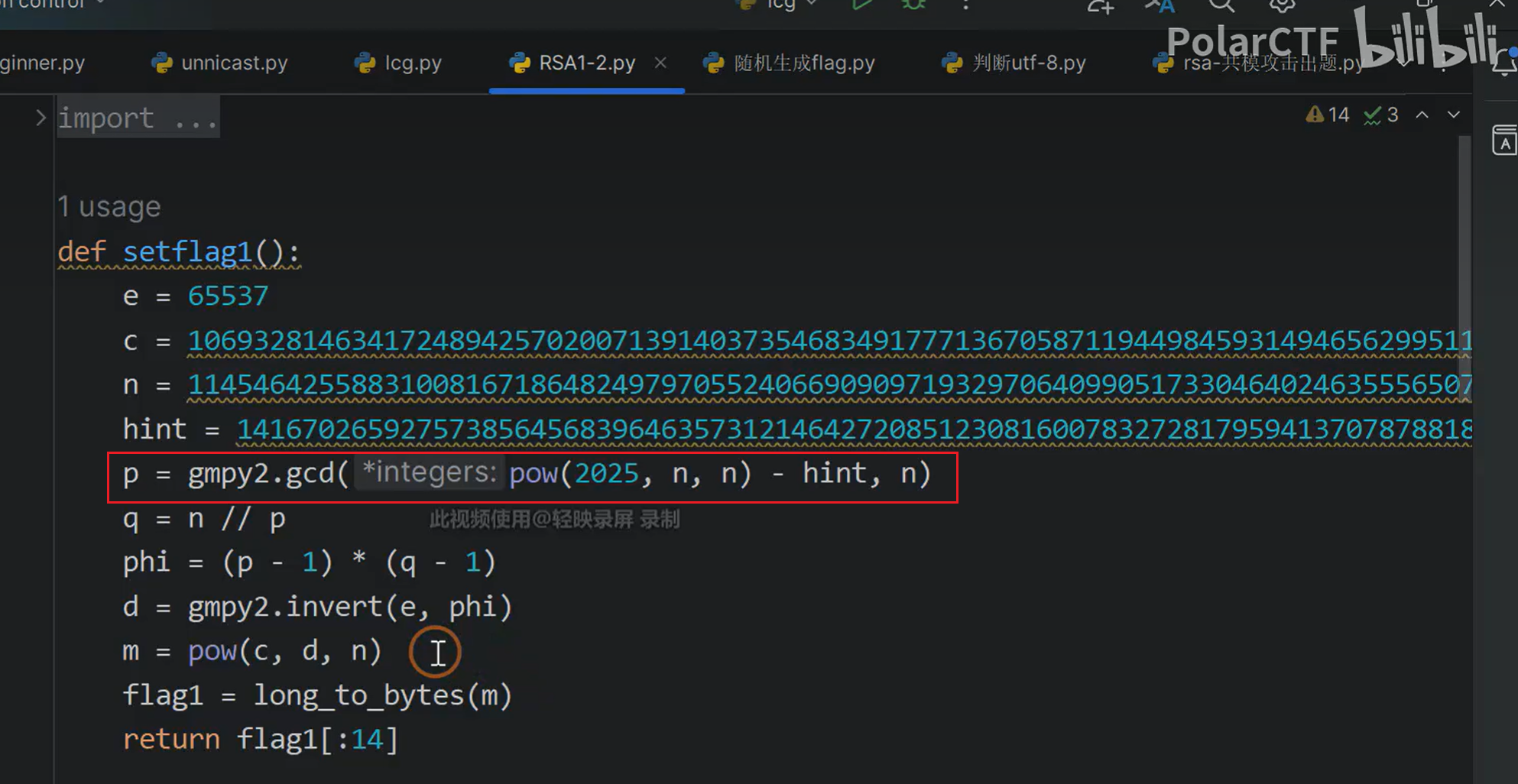
其中$K=k_1-k_2+k_3\cdot q$

求$K\cdot p$与$n$最大公因数即可得到p

getflag3

题目代码

def getflag3(m):
    result = []
    for i in range(2):
        result.append(getPrime(bits))
    p, q = result
    e = 0x10001
    n = p * q
    g = 20242025
    hint = pow(g + p * 1111, e, n)
    c = pow(m, e, n)
    print('---------- getflag 3 ----------')
    print(f'{c = }')
    print(f'{n = }')
    print(f'{hint = }')

官方解法

分析

已知

$hint = (20242025+p\cdot1111)^e \mod n\\ 已知n,e,c$

拆开括号

$hint = C_e^0\cdot(20242025)^e+C_e^1\cdot(20242025)^{e-1}\cdot (p\cdot 1111)+......+C_e^{e-1}\cdot (20242025)^1\cdot (p\cdot 1111)^{e-1}+C_e^e\cdot (p\cdot1111)^q+k\cdot p\cdot q$

化简一下p的系数

$hint = k\cdot p+20242025^e$

这好办了，我们已知$20242025$与$e$

那么有

$k\cdot p = hint-20242025^e$

为了加快计算，我们也是统一模上n

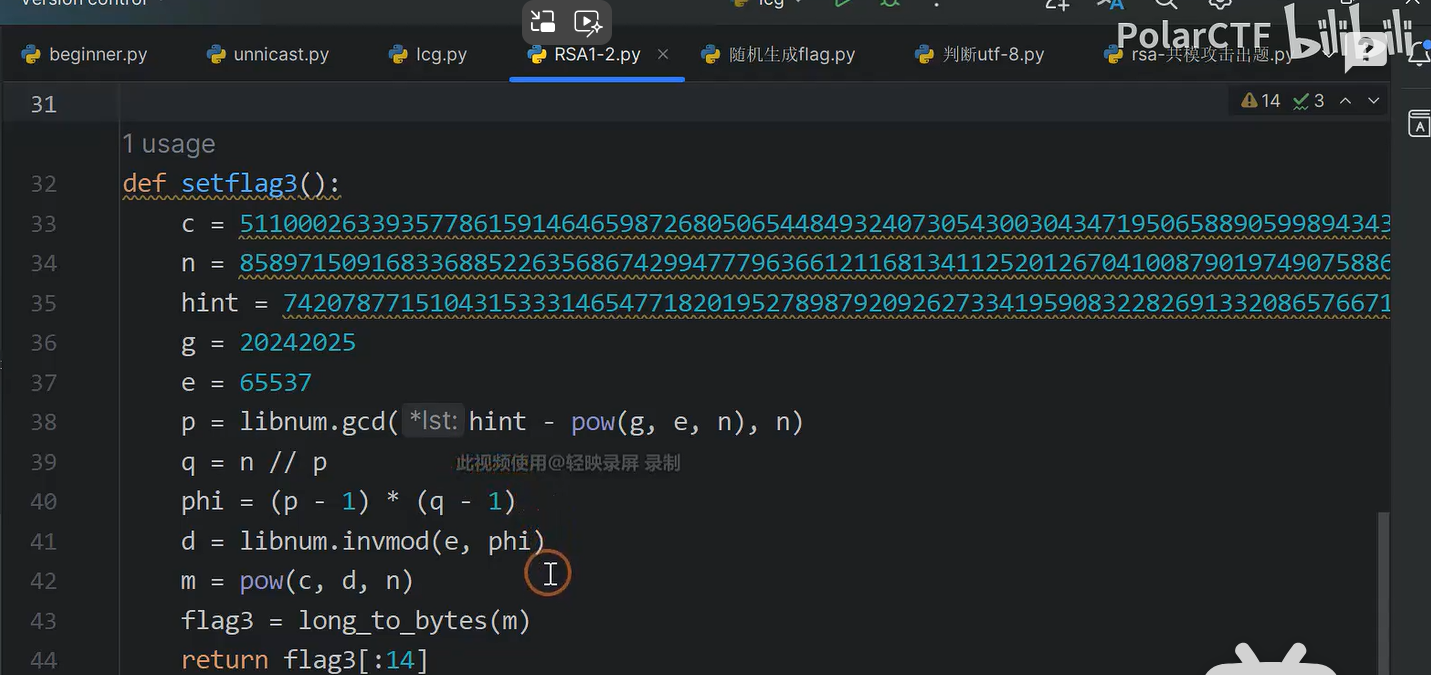
最终我们有

$k\cdot p \equiv hint-20242025^e \mod n$

求$k\cdot p$与$n$的最大公因数，得到p

[1]降模：笔者自己的叫法，

$n = p\cdot q\\ a \equiv b \mod n\\ a = b + k\cdot n\\ \#两边同时模上p\\ a\equiv b+ k\cdot p\cdot q \mod p\\ a\equiv b \mod p$