2024BaseCTF复盘

2024-12-13

字数统计: 7.3k字 | 阅读时长≈ 37分

9月份有念头复盘，11月中旬开始施工，到12月中旬结束，拖了有点久。

关键词：copper，two_squares()，discrete_log()，拓展欧几里得，md5拓展长度攻击，矩阵，分组密码，LSB Oracle Attack，MSB Oracle Attack

BaseCTF

复现前提：要是比赛中没有打开看的题目，先快速把所有题目（题目多就分块看）都看一遍，写下感觉可以的解法，然后看wp复现，刷题。

week1（没来的及打）

十七倍

题目

#include <stdio.h>

int main() {
    unsigned char flag[] = "BaseCTF{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}";
    
    /**
     * 由 (unsigned) char 决定，每个元素在内存中占 1 字节，即 8 位（8 个 0 或 1）
     * 在内存中，“字符”保存的是其在“字母表”中是第几个字符
     * 例如：
     * B 即  66 在内存中存的是 01000010
     * a 即  97 在内存中存的是 01100001
     * s 即 115 在内存中存的是 01110011
     * e 即 101 在内存中存的是 01100101
     */

    int i;
    for (i = 0; i < 40; i++) {
        flag[i] = flag[i] * 17;
    }
    if (flag[0] != 98) {  /* 下标是从 0 开始的 */
        printf("CPU Error???\n");
        return 1;
    }

    /**
     * 66 * 17 = 1122
     * 如果在内存中保存 1122，会是 00000100 01100010
     * 但是 unsigned char 决定了只能存 8 位，CPU 硬件会自动取低 8 位，即 01100010
     * 01100010 即 98，所以 66 * 17 = 98
     * 
     * 注意到 8 个 0 或 1 有 256 种可能，即 0~255
     * 且取低 8 位即取模（取余数）256
     * 你可以验证：1122 除以 256 商为 4 余数为 98
     */

    unsigned char cipher[] = {
         98, 113, 163, 181, 115, 148, 166,  43,   9,  95,
        165, 146,  79, 115, 146, 233, 112, 180,  48,  79,
         65, 181, 113, 146,  46, 249,  78, 183,  79, 133,
        180, 113, 146, 148, 163,  79,  78,  48, 231,  77
    };
    for (i = 0; i < 40; i++) {
        if (flag[i] != cipher[i]) {
            printf("flag[%d] is wrong, expect %d, got %d.\n", i, cipher[i], flag[i]);
            return 1;
        }
    }

    /**
     * 如果 flag 是正确的，运算后会得到上面的数据。
     * 如果是实数域运算，flag[i] * 17 = cipher[i]，那么 flag[i] = cipher[i] / 17
     * 模了 256 后又是怎么样呢？学一下“模运算乘法逆元”吧。
     */

    return 0;
}

分析

乘法逆元，17模256，用gmpy2.invert()或者Crypto.Util.number.inverse()

from gmpy2 import *



c = [98, 113, 163, 181, 115, 148, 166,  43,   9,  95,
        165, 146,  79, 115, 146, 233, 112, 180,  48,  79,
         65, 181, 113, 146,  46, 249,  78, 183,  79, 133,
        180, 113, 146, 148, 163,  79,  78,  48, 231,  77]
inv = invert(17, 256)

m = []

for i in c:
    m.append(i*inv%256)


flag = ""
for i in m:
    flag += chr(i)

print(flag) # BaseCTF{yoUr_CrYpt0_1earNinG_5tarTs_n0w}

flag

1	BaseCTF{yoUr_CrYpt0_1earNinG_5tarTs_n0w}

========================================================================================

babypack

题目

from Crypto.Util.number import *
import random
flag=b'BaseCTF{}'
m=bytes_to_long(flag)
bin_m=bin(m)[2:]
length=len(bin_m)

a=[1]
sum=1
for i in range(length-1):
    temp=random.randint(2*sum+1,4*sum)
    sum=sum+temp
    a.append(temp)

a=a[::-1]
c=0
for i in range(length):
    if bin_m[i]=='1':
        c=c+a[i]
print("a=",a)
print("c=",c)

考点：超递增背包
解析

a数列每次添加都是大过前面所有数之和，

所以从开始（即最大的数）开始遍历 i，与c作比较，如果 c 大于 i，那么说明这一次c加了i，对应m这一位二进制就是1，反之就是0。

from Crypto.Util.number import *

a = [2487264674516612702148381262059366937897201508455413114345031288894980789076145147579418259432661232747375904997965581530362268904008339124626472045717075482791021095030019783589425299870946373246221582957232862473515, 491733695728183987781854883946776199363545034763223630648303216239781071808983441788738994635864262288104702316190256147614095355462666760091586746521889127102395089946736744234701020777747486645716679961505355358205, 110323038758283816811655397189354730775114318542406507944678995133064353922234139010858233544980338693080719766808774615216332973443076471838385315798081800456260331047745824029902641504699030254172864776140503685719, 21329601123439484788549839891633989762344638209267595412456647269024794605613697213699096256470155035750114059504925376661660484839061252258268241386676023785213539005867805566800471943519247336183762390966700950019, 7146972597944713271040951137457604863561388249875746261956055482229418349264570561740906104126974792505856583850338097727129246644471065603435449813884941071413766137227119139128098345457922432088128969598942863267, 1346101131622672931978096423414991055086097907048045187836881598919564312718270178534519827267497280433625574785132174894812908583233359458000469975702103413693480199742325839719191134247009906270778775450756715188, 431832097768527518676165198802192386603746291434967601504548859319580699889723090943427634867984592194172569910901514799190511020246917662162535632202054961537707269684557393598823535364874075052250490284484829188, 140385263282271996264759155211641776877746297983736897311922733831813190094504225023609340831846735540994403916688230922925129855025970272950216444321463493579227283703118512150491635819942098587286980862817753505, 34223371325515207445588748757581712557393912157235932688701226001484995652561037930828670928779595410194265999875772181711329727812185265441887453894003309876654082495957062628413923487565276953961953102939899664, 11277905223110088306111589808536546872836546320235997789453098291242971723694602770076671423955063276020078678714571127064308764611705435202479293805661470178917099557275252963592432838615626750886647727435412727, 2615533435460831263145388899927800470846179005257762751742107113431800042995970550154282940437470113325491219189765587324789634252029440596113709555932091761129000675863727140738692649309833681187804499985953136, 936680841170458882946412959909966575946011948314629933325082014426837165501136249855420901858482634295013806361789689361684904674438042695516337484436348646919308417999556756779144910987756875858573687134864914, 240803995584844951172124454225548986410808735949094019867567366838810221297826531921690948148961695516283629928962961745839887826049348862278548294987215333063020792491250359616172365439958324315638641990190536, 74980313650452416147684959971591530004150916322659108850519926847892455755211157414650129501071119906261853154503022754482691495645170933619292755026582075009055897885581671027043347130782615603358690889357969, 17373734350550516610959609643239951947839958095899981508834140825450716407631617618229082722622331706459216379319570540046133821392793975119423828799726656124807834541043219269949459907314628636546219059231483, 4383939698435145446949414991318424065438281430941348230548310095735465803169460840233678696507780083107318568406471009158126616954496458697727524252433591785759305622568557705826283690985480130620325779855269, 1070435075033499499988967771003353861621342562651011567215908784740129578236135452228720299864117045007232989018924013752836270314752592099997410344317383430641687448457000377071747633795773722163076615405153, 354613024399513291150023928129989293929227226203084151945112636505041432337820329935805740802403361855625313123094613318180050195219366366832494130593248906011113600242755768635094775633827342114020854687801, 82597124584081826710375601757684765457467298282386480837692933784824657535317108286212691529276214884031365269733862817274058538453459456296256548913748615606422415053313052283494323168620576805637766138197, 26135834190257866104316629323550052649627679758726229473294221139854796563641126471998920211481501156701889782668173105315082084500683017294728437322818254222939692828669475566191154442279318530752996234399, 5321914533271631715766698346734309258597941523919808971175049357994196078126479079595401724485236733828962687678778457409546781470810737250537642200901652790857563365204935103019528537962033407161035692676, 1401112116815344363602973427355047116358185953451255358550792547953394603648490800732761959337994181037602301212276448178218413428984435465643957862122433848889149559184391769249005008972240636924677483332, 340703164964920022751406615239919113589733348338271455697386514814772581315065581482054968704086006813510346859307625729162886049905513425065578320526943584411252201523709613325050800852296078315276309498, 87840565476176074750781589683807196881040923233689789764972859007886298300522765664170224177346224637510402223797751637511990096677274023769380478419759017880813713095034065541851821136431753956971681001, 19670793194720557916718563116693476958260133378839723765611437953301903581689095646338017322208705125479649557618768892326788688569445543579968049624743997901012938768052637463357937838813048475700143702, 4813717864536159278344281889539442680460787707429632446095662166356039450500759565004728794684170823084248242129657936118206321365817871353015182900801593481805141407218121604733002829781487535789180828, 1042206069053701098495071546906704343612504895408542932593774355364200288153617940373728364353536406373351075906293793845088075847011440543341941529120830192687505151588415115374221938124244686599669458, 194044946903756616103043562433809500007183272927392950867023951726626302681204141127037211903589021504233703959475286805099197368181117710043885464503673129287184477006142067195426098588591382748102539, 57242060503628134854797583503415516863794342630010325140908044397602380211468806869876771678223543893631961137313994861319272460663638480876700367769402916003571424012128837346480997355093988632012775, 10220201967005002779370447788097151915347020902180766203690278038856770790331091587750957262611786369059831723020056245241984653662463224025520044810966000669665537134571188694822388194379280786606327, 3267926212173074655716273983885176036956276231571067023300127600981173234474770474267538130720791055154389260987137327011230845199160118826368874310750622421181065045300794979970673152630315803973451, 664310922264744733608679352162235206229153782441085066286192469594499932348386155418089005696350197905438895173077254739918594652439993237866669330317791070351667267902119216464673735535997917820053, 157621450510303034999027157498529810254434467859123877137482107910574969124384732028159729373548578204828393076100787322321913754468400698891584836797607004658385107761645961934718993971913922689493, 39332477720879659647769207180648194166511069149312182714850691343807294060027257884701895063257342090729165323939249852666973310856943035346466688523098612569329263778095249692454805322913109933451, 8981431226314577645818078061310516067058739244501260778838272265495867618491462415652789974290152305589437388668252286740099675804549931870318361834902625342381411139234786285243806607019356580655, 2112396066721715241251602227199629841249291526749264633946336472170358658345723532373776051582626845585398413757777914886165302637471620129930025840435283626998895529130832700898103592084193587990, 469796330799746978963007177579525242476491475859713462679382870110198758612531699613499280185379426640464846165230615898408348461001941619050157303936273348173453633557613625134687931175489772308, 115039894603762374765072518903656214032673578314477265152318302986985809844170481821167559173999270345678822988509361838537021290790266729339932399789571955857561187896624119148469524606927195502, 29664847413037439140755929162295500789926130685594096951097063583886105875553862215342779333568726148068998390489061260679772397420854474310952173916283562144502155749545173676547095974974938801, 6556839835049647931901086051581445260744766665407776927047263448383041272915616955807464961262297820118065353994454969038345182131864552405100904248845811998006038518360062998811216993218123317, 1777902487663062541759851155686901732751487652837314110752529657038468352750515100993079307083868172100714925159868062197729467104948375724637901426300367514987134187716080043905739938236648704, 496319028827230065370808145407239788641593404351668605447266421139929451476993248197319730317200648698252327668625409509842367526798038085336803728242097138638139634601057690936621540950362878, 91859873982601930765698107766946424315968932113724973875252752520495744658349166435087906664763198237819106317321871232725285852613201351155535304791295392982339051653723048621713854087558299, 27416797198170440695880404003135961426335900780086489077063102228234854286849577430053665684665123525576025865136178905344946412182398068100227278108238228179476948006111402146551358956042173, 6618792570596090569883178232621713030844697317972184177900266954498675602890666553071207714570183352868264445779550306428622314821163774496224109073830696331713973117656394498431868066547419, 2170402078990376080093979069174241330730093169079857263825716044536454255816623476318486713531051261924372354329543376436907081387161693951811518904258013624768207438418761774847657241464116, 444068419739995022918617734805868711289130441640491361059833564963918508148289061718666452354434057970227476744547047349557417149242164606932560068546338531971271707670031796603537502372902, 116657711114961473575551110004924695540253659208616449841332120251303948007722209463493630964437083428655981974738051994193994806043789586554127478932520376572981058192629163539170482099439, 26060438230704097273528583087224964538829526126764669880723211182150736154082956489319587015488424248074673973497150602509972124276820315641896501503925719577821672512750083923483639733416, 6312791407424911633066282842976932623335914208291314848182683302453777089215292160945721990083867179076948154652506406356338815828714441906485780965753668277560566183244931348859397184996, 1692738421964980687206278894671327723911704272751755954222196367628340111939187266884312772028554097537058570911615150944663230388612366056826914851034642492298594744849153229556190046330, 467525048501123667461709936020772038812998605707446973687794928398759672463134111033796530786478727006399722869173671763892936977996495279695995929887621412909042553923445043307978487073, 100524774903368088338735495212617525628101069016243368191042349062731422745652851141040067275932170134907320208205726289799197848585810532178559348960204294517902672414604810447030596048, 27814678376250636475963101212563090069738325215292874239553841311037561288624279025540601779796471707609056593491462913915467359662214011975515860736192625178250236017806638891058352841, 6146583639189016851959336110111529802617165794295583668085087256400497268514196451801697302172354876150306785802188833007655768181472221094475392274540015787948511952367768046413009035, 1972647620592074216061102097901025152958921034850117568363055778941629490654706191168761681590445732321415108675787531563680577749629570660705072798303247953275401784690900022657739322, 371444236734952267365204917912482218024760669256564601735746557802172061599306636753624221981211002583971063750448869544186339158302695225083644994003958727288476784454648096424712122, 122254251587569792335530528509722911970032904171801982862469794399827245263786995733489731913997837358853070479769024383526380208988565918719151600653752397319872277146128837497328015, 37286085540618400296289156352820709922577362907484951458689730829327977274283958429361031670068907334172105855310654077662912181145565822690393824208950538512990718744603086462751297, 8960386121829638279311227577342777825734976587843199435094340053720338004424184197136819101116475086084110882985205105967675766957208204488229410580925549838579346975088433058825112, 2276020215301107373585539745757682715066838555468744061772014192384015274014672056309929648681686089838637957127768944113418121587630588726390948566064269910008396907056486696440621, 607349939368134408551415861865227396073824635286316486245465114777775395388058059102705505424561001490318248134384090100571125911216424062773005875309952406284203774537367839133285, 119036276576206703263155095063111697848826207711313825926870015597766389307963670003146886377762517538032971265642879985310317695973899218804472784113163457901422724084711780785647, 42030777748108550530459203444475857940945563824576240738615672332753050069206966495014628929275783847295884969372071131041457167837216841146848083118096773135990284469263324779443, 7801996642301319152692691810553695688255137357013588495692283033031549008190374987427339686278893185224986120367594016951691992507271905708595080902010159659368839867860433342236, 2208574074019210752518459502962754515153645798717698412888529548015314931730564928870825878207969197632997431492713572137381185806543942907257429896476484304820878553303138599159, 768875672280773738301803816415515519067859985949784777815605972358140605222957399855931295900483405997209014872309627261455336173608212560504792804732406159988744626008190591642, 213430837881757766520777720690227709564760977311522001626864091515991137423909703305978776728094360822736833235760061066314816749758660033547207607953805341923438394772222356568, 82360211831711259567147082155555818156999516949891879514305397375226376936714506922756403002876731807095740268483307937613566131364594612432398098476300712735589147781570183292, 17749505352232170648277795567698933594199437689182764405380407013992895289676270195878470798816715217377777574478356564936400974585960088437473753598924064324383361905659789789, 3427214394932046144638723931330597473316067571098072662894954825121393877991928319931449114219100671521983554547487355301825989691873309784465316768877146988849237541879345997, 1033902507229521469775736346351634090020261583833297661608844489398831364552754846127512235344097362890795464047384509362185144853214501000183283440093026203459311568816825264, 224896235915885231383021605802223120291823571580780275950317681857821908865357784480256946962966353978144999197255874549242776446126658379098611152585008158970159741029928166, 46029158819241197707530664166476597494824578315547299718547883731820892091315435238631987346971891025923179798692039448953613556744177038196467650472219486883115951311114343, 11947866502696456680811378187645438096064991719463034800178755900009558951200835612294081250719346343143340755576335021624771970543003065673188450976052831967872919086392740, 2920182352645954475250456149302161189384947754266138653194940049989939156554780361528842542799077656577372777863627070726368904843252451856963117841700429655465449705784298, 641622426678020294248348183140299041659157650855760105808225416711044677800278294044700367798760043786235745613510792462327964867426046011657009528106413572140156175050547, 139954746021857963632941471710740997948822448809029403690252968784849647633362222415971470082427919553489814062772632095710992183657541577740542585479640231081279442703729, 26951287563812328009402867445459718346022404035671471571180747182520664735617063468580188663385794364598479725800534646437082877207222254951262061856164914161401031069085, 7533585444288704788707326472044821719148563540561950589462107215132713320228676563974287003223326227564110259498308322080055316439031345783355395296729881160340610419798, 2276681583409260736395242645263289467585348662731848036224090877214770286189504748163492790260653720049576572250410962278647838121717162502347694787530301107754917965930, 474556448905745036966775435479094252142291985759634322576584740921367165655972599891226896859675668151114091970232772247346351748955558953513984653925641106869750480713, 127434337967780172994097939061090682233760718060985516805855544997040535343689397647620215878303719159525314116562161004671399396862283153119456440081266677387394513825, 26958440398830097157570752848820597974607321452122682350667898050790790872944229259301257843111978215025542048968699222294492807645241856446964337776714971381969501071, 5543555284065922229007474385783130130141655633965977061928013317537397727717406514000700955159647395591026117082092382033235800387850239860460046217510413778741145568, 1234762639172810584930296374422356813288496696923257612102992994614585199225028932857122231293467541131628736229833789522239025569090130126077017761481761935075168095, 355466248406445302867530536283270751070714127588124044114582631609659246249339560304163152323418724390561360227173698743244037301264764126798143323643968965204937509, 72700233281268425015457883799224003903351225804106120865021630177680188790291132871915896124460090399131402188231983457135950533458784941828330878270977967060216148, 17316325779212303492370685449752299828026183539683998725619992507954441121758510621171086796417805607101134043617316264832615245565516418608812080799316990851625705, 4045793926070659592750134404331599438619282956075192844401269281007613550701517318190039173492631001707043977026685514125253560526115949503328595814800145874763660, 711093850172488751248536015688936346283846062295071944527029992467516277719725837096755918337587878576030222851749327532666344838291776707230618144013255672878802, 265627118033654696712457079751401631255125309014812639375295118794146799198801006240800873274048170518660448221821727034749291649708953722421725907035286053353872, 56397799026942637682063511042055387061218525595156363606895648399263418939712512484112089481484737116602512227228360835774657959685026627558074305176995845647003, 14485314789957973511455116454157965523985421493897618644045918045972073878396047755360530791556364199120111093825046698573687446383611922050184839529827282440392, 3550955573839595298078922255066479093374448121222507459840552079059417076208499387361330875700156148993662311858100125881757983588374422578671684157194578005699, 845394743568277367630651838202283372116209637644259875312243046465466486130071115873693547193074995290146894807692302774606698607144257685615262061054213977420, 157730148886711208861332893525227881346167845596707482474187376786153504516831765170538422967044056418676212271368775137847308449974344069982254963969728576186, 54972881967813310263623651713923315210166704822071760933248319000133464676004646169143078394020203091841106960137380702725337793156762085219469872257140065395, 10729618624425932454603285350456338562675184367958955898413107388221142096410983819404349570576694967179369846493834859543515755779034404675292796271503098978, 2442709998183758153870663320358670148543830566673551209180788899834647749860789589565309923762896818608005296106561164431377898506019097822580641263331814899, 651590036376284619471743663785818577107718418313829721360265583261583596100827943422638184205536113868285291626431841044058974804223249221103868269005376657, 114607798091152645971169174208076386390725220406372401915445980825934238917993417913942451617626679858301802459311641056076814238046173194524157303256038150, 39902529162554510030314089494503111747276505091248405060746015077422014506338256115473236342993594864048856417342484086620483648018566663638691082167406896, 7696036409658331229292571646244718273466046087174912598857625566056708582171413470987556822776798859431848832604237853020082821687940873973792941059899704, 2124793715529138812294972358553948624813291392446651644830711957681124971135340690294893448419315140942986852615187098678211216431027229098600530178187333, 658384832743376570742078380839633081933064245096557997421967190397377225701314189557712470669358349072689322858650074777626830988174808516744296032918846, 207441722934708037755237631720378642887937120813748348023809687455047615244353892880515039372882445336126456679753369371480841621878413386189854105557570, 46120989258570141716198175239164426659655378133453203231982537688000264558364343582463401621127725393877459942514087061448921695021828660135004811441077, 8188249463851855339650372248928765967441086033339032675901168172673586603869217763697984051550480433177801759541580074823902608731330486865652085135044, 2937142904794524692633847174299189664745670816742834573158221153146769098153095208026269794290966633578370921776670433893125934429015973900770183068397, 733124926365921400367689082582974550222406734787055535605162687013854196685186803977001257147200683812867023143593280536908792623212121135546302252718, 163278402453599131564496240174531690514528227885644439879148727669198836851619817419582703102053351987308732391369947772790306377652049104175405389057, 30247650270830046327693354982611104496891052070130966758534212809812843335592964533296290766840765263207385481421035739473846342013342141171267959427, 10078130422940933339521748812234495734268808180137214319132992860890442263439248960992021699437860319479050323778157839338656439168670198619111143719, 2468880502161574512996214909253394046701372930781084997897282377444297398943413058653731620475409298189864459900922031063170285510529204509174601472, 607074026100427506196023135076433955199278835550407310798426497629249872001552107547116229667872950481628543662982580322754725261269013849906534673, 132740473918237042219883376937810235079740145884708583638955667277623190279830437900121550989480157388767941856419463040395910600481643868918183256, 31718510456640085593521631697634193356173604238387825664787000835659167411973149050707246808351118400835035866343214347384616969135648635282147931, 7013023279079169100512494613396045516189395791014739872279083083144940194186933569894993097804928064121695159201540587912810973411497923430308118, 1771185586112090213616219590319917086599723206748079096836927259082387415598439340193771966567407719988569555116938671184047274203791682665544114, 397374970256811388188624914624139083024782079917643579178513419907217677561151325006437923068157587425558261984085274694860016959461272906962347, 79357052331733760410996870451429462826990142415371259214931967883012213322689987714484368914655142353136743730816759493623445282698964105194007, 18024995037150399824560351471574943556440673595591374226442857720036395804619368162299007566488606118476181051500800792556435843369345814420200, 3672082813534614033824027501205682677746304198256311647201407880518658491065244877413146229442328563967205873649123895823789401080903874966058, 884390448367024106697977520994089114652140177186827650340642302821550463666402143376715117683073225822100147575051185094558637911933790548300, 188239732756327819809744123998273956373038631188535307108080455432157193929576323356894115167616675699250266852372722398883063108283627629142, 33288603989729116913271536956952173835445978966530730095436444955036538722332958231617041802341417062090911709863572792283326143337721274355, 11485733967829072841907653505652765367596185911550254707130569392647462332893031105105058197515848740962693154105512628726167266984356020289, 2403399291804759683718697201628718853672014990022411946032431974098338948608647899389041474778909482165700212670301626696886803147288043249, 511319889754958068650171413169799880502913743237143323338990019288960892229714861654882544537650773480294037968794797914167989453965720824, 108151236227275669723663372909233127249406930188286111418173641508503812685900937356143956513296377001193855340520507635261983173020133040, 29238304319413057053313068686030250753447165587962843793828466785518433534702764546822180884428461976687744929459281379124786742084937021, 8710806082582848713173281808121766793059207164795295196447513451552342446919958461280536897422363560410120915054864290671091109422830007, 2960745852030782790607427333914261375033099283529370879973360161495226124203100530063141357601421786632355173585713266548540973431376582, 604226789553326438591187728019722484152820159976600984629527520901554123057786334839341626845330699593003318860611284025243121271706983, 182601602703012851376129630760230344746014108213070190831158648995503303041568836468914587260292443510296580408749988987988496769980026, 45452114165544367630569931330797239179068892066478030202246828842399491816831847850747717090783448434947452983100492335497009639567888, 17121905765418035275547423058447462707899580001255272989656046701474401090015657327101125412277786884745764423250530487272209339058447, 3774603297652275052121496733944137560240160153708941233671122697937317529256966828765637412706299259386179629160090242954994907929332, 1060720547441758622170146447289706124200025617853186951481807263542360257370083864882158715152433273118314629121456220166038646613297, 221968014150998259820244482577203245639303312867709655818056071267607816968641371724863025295597993367786164837699315327363092768373, 48882714266352303994499906166362680249387918980441207673706748487810074857456907593421757139320785593117603391693650930762966455968, 16202448926627445820838961561455164462246910065772244580677765363543397691542726082412061203163218760307389834156275979660359394394, 2956163682419868606126264117158250029934298756926288053091609992334385653684466888852763393290616941805759810929196668548734379973, 947743414350088412833104395509485078494688169216314527117041568424743421788079617145817207736081707175649820823460623353469499129, 184945524926843220565904193572688427321550948207655453104873607656563645624884025013598624332554709507217938881998831490973926770, 56091241819606834802888641120709675472905317085277369060569812131174812302014447128355020686805930142925377568700991226583887786, 11342476554725825973899273577573419030806527097049265365675861670559660391106730894000199354064208522140305551746468882526930218, 2402177443476249504669747634772796049517512708172380623039160322117732888388776939986309881254003733945369109368480598991083692, 779694676467776330674778030069618028430247798034244061629255618166403221248637754838157860401196252119142530084615889227008718, 279805151354990313327069866270353558845137298807826578854001581649814949600343606775647790956175906533124785285484676594205727, 71475104043185673882357779032282210215441549654529833915666511795774890652222328738683786126978390540777959958334867072773903, 17943539235945014339231354558742830502206047263873390682998140665294407299445224663761111928004278268665005924991145357190559, 4644026442647371851471373522652996931494883964189143247893482852205071445064380253582641516905658082237627505163407862645664, 1409644155578077661014560265925065735043498896729842671302999827395230787557009605337358883198670470099670153973385533319619, 323096734145812043063935925026236730750028036642046031570292345040624480525514361785469029998625026693350812690921739556759, 66490109788591511799221912380563668027716398810544644123382175383682357229245468554339935745239347569290928368121481198120, 12656292548243054261915436732277320096081079272327419007058490559709461117024442299280829706525636594720337557745657188367, 3391681366475824837488092758715214360838073187075047614113065989329609613896833473414068502642149439870471691863634629122, 1171517421153263625675697419132009454686117107914679030403775353063155717395912120634642665620725468223446139999071277507, 283703308943571467555327320427163735194765821724187323544643973406396459830945519805247147967066979142358739388094356677, 68051202286065965847502158995164914066216566669074127539650532219749577216638549042842244710379907101440823172129217941, 13657391854992511108591836048816405373941724899814769682716923188133130484869138365241075289816576384008939639840185236, 2883783693644859186835460708048379333567917588026714123591585397758887606304693027342351097912118721134282551369664243, 799049413981621014519709854919842048905323519892313665984919603393072653972864233067257746232644641382453549991205564, 167323486728516981799615013230008131717839880066330604897780052101994505570227406902019168715315935265773326851501787, 36720821966367632835200966450053402442515187808387796741238632349642200514749124280117021313827183586060369692397742, 9231349669963900651759770670625059190403421490616649578654575717995018536450416781815824036250202148465899261409814, 1782108859562682583955834770956766771890605266822317978330465547356702234978432274339716401371413673051273821401047, 403558799957529775306903388246707975744649346938130151765107472774892029713724284184220469230250620098654222513187, 113610170795802770344935864787382347027936273326387062416574602249889635787754346617875788451115772661826280534521, 32055073799513070460127524930885397197257512625854036561086683809899754909243064094359316603350553060664792782962, 9032924934526196049960770072668776382612241442724751839457302023155061259650364280524549081144893790536494565021, 2017862790729520323724155794794272872202696299996991444268875260039652843714149080734888358373743815054699872032, 641989462295283575733593919337192523868529607267791351139020713122159499889249625918896534847416953951571198300, 128576036185681041874919451733195397084174018792730182604376427967040903314850718633946179141568345684439398601, 40372047007036282320578970360805818319565465833073029617047122562052782556856211341854983376957243551410081742, 12690329041364261531787667832647179962305068888653710915257119208086200721695307184639464428289081103144163044, 3561839882694824398822284966776610177573484210494611237706713481725365094327241161248699081978241602830178596, 1199938132534089466501994820759235969832300222872622731608847912038243599132645129289586987692172765041057363, 324263436138121201088338125064781061780131145213294921711639118717892670326681104392825089385185080492440484, 68312903907509568411987755477707268100466381276451833349595552008166402404491773244111478626617324226539375, 17644820024620964580235818915132121042107943132825887368503777072488644953818352369186661300059264368686602, 3506176982938427175993147412444392161707218066658168782915638022559988465482121419504891010260766228901318, 1066127911891872518349397911557440606663336809214920827134975446907327509548040800613223772158827103310018, 226192414853873324160991825316404956087309825251607871786471768482769238181939189651359979648153657144702, 45868481610678874924581859998825662511897619432776149300471637861901025934649825592930301843850526560482, 13790618957198333318923230203705633437848971510707911225277092048085966476634360389032477412386316672075, 2577037700547459915849817513069936580425167358802123937052546118913600453224885074049561249688358836828, 907316011507113096967526321014989153923826069305244388586962072152306166058795915708345202709057953005, 257655812504204080571300921288974779044004152926402846615682864861219686480771224251979519937398150021, 49251062839756470728155099947305937498531111600022908848098152154867828870296984401906907127621922967, 18003086576459067165101290934987020831800807030229687007784917512221091664668503037255416369751058381, 3931602604129427365537886268681901399659904652265314628365560645602702305389347981284422957262198925, 1024271243554288667730540660664163792950639594042380266463713922650987059456833218457318808946966091, 264399551848126394660403560510401104363977298239470868728218368941030448200247464958990623172466340, 91991457278474569364064153570190123603908094841658212918408559703533962838464377716405517361239718, 22400319343956127928389329988299680966797095025488025868862978943959831082472834977311350142227326, 4054933925260064992644878588484342847457594792015796931877255389193313381697255433801823807489993, 1563931191287550417926830376062569859269361644002382824954373333292013041945346281280805769011292, 343600935590550484460351833584964172817805330710096798788745676605896512317351762955463013247649, 63176100013413022744650607325631187438860827337150751513958540819158680919377176592820951694123, 21461895060447171957232560518498142689748550789857829420960180353599240337920080298104122001920, 5835166770039346718590125171268445418773015279002775708686914119655634953623824713817863325421, 1583080965885530423876853196443645139416147803583378489670913938148126388391843537295818940207, 392027882718889629138666367076395194013822284370187648811904450742968357888850048132707951624, 84773060845038628419287336751649666625561226450930810787040749330985148718455599359011719538, 20913329354023188439880157138010537207897970146456506518137268768176475768733880753458923347, 4311750805563893138689876217833463788577851583828477282279295599052168675043703275872499679, 853899685398867377607396879875326827128843982112866203167371936104484725330862023846437598, 177330267045126383717093581983187474779454406408201086941455408963372790398670000549267776, 53143647775046286515978817675952110384368487980955438888997975610432428251415059859228454, 10991259161865360146194812310045803635018376660538575719261554366173833834812335245373835, 4056765217542521288464908532309700817396778995632736813131981648221349714370388148127516, 804624166261647601714189486709310419472244009530705820922420809512944365943834561839229, 221209387838524016717980366851546408106123634464083126244578703480033718962945353384984, 44893426704852156297812963470050296993434463573414592728231358819460836492051444088309, 15097276880249572944791099185953982641176811310343688646744220558627388586126270884093, 3177547688411513827329112344846258118128928380413096551275296685970663730887380521208, 707854681966281587817169996379236533896940250761506339446186239585936846532007717960, 123430766712269269314015844444108981877839453341743217081639119599583069918979135631, 42727196484340883716428235074652898935106385756024360939020725643288512665432787419, 9795023686113954751639542218587813833546340682044130681106706094735594753449446343, 3333589652095912448402556417544763364674016013042330262047943676041390880358346180, 947455010581251264347248926744940190279860580467728251791365397084078291899564124, 268670018298046298594544067046438306285322924770238391595093977430279476868065240, 78094390422018068485749659108183366278694042747549744891971134188665400412950020, 18124918094760916369648633132238959364840331932070152769613739914614309846704031, 4241888706533610079212359644998015902376872441583028817350629704555219530448753, 1292864973632566395230008219224138571254648896695439011761255646000025705327047, 268748278858999280597005392622004242197468731403889200124673378952297248513604, 88509143938000904019404561563568039020388387086033088264015176342184836107961, 20193371122440969904693011623640235956008535236609083989796068753247319156032, 4038600180280215891988824178178278280373636611246918842044528278230564207261, 1107150907782944887892399335890628523766269912586346493641592121812091723247, 210625186186013434779241292600805721380717453215450496819990522919652412749, 52953910211550391007013147620224873533688473472101985821194501496064403298, 9097555221706291288743269232756819233000414675958515393645941994120605160, 3429649093597174301305755373533641028744892761855146399462989664052400884, 741640028601865737636894538300654069448568041784703865806900024636263858, 137111267993711698795554790044192357770629382096307382022924712860324239, 38616149627736424773611788634842959989120382193171456026729095563767415, 9431485520373346422889960992205054090491173749526200420980321805553690, 1992952778532071559000019699416705938136688490627773967637839059076015, 574194788106589082411518870360486672683587224354718671901248024476268, 102609620640057348696515220693089742351613040750651566890644962920462, 36268823254475267212915191076327557136209959811616783925907478300982, 7567999544690811975942075962292580482677577353162367723788797894980, 1874140527739488453786828468118120241481575966337619572680165251377, 453914446353792760975691426663914252084437914832347163629988619705, 165150650733410175597931630292861667062273243834275274945484646602, 34566163119600685975060339689452757045437083897698838710019239494, 7694148541008402030841753047537726531717215585386379181283251145, 1697576884850411658454847805622249167935227079092758267244556419, 472437807783179983228633641986010243354676995634705949446120356, 119409918075506001971427759705853133156186846892920587610723175, 25613263424766799565203791718547119460962423676387668942984591, 7805142960598461841091346841458786166600096726425068620929337, 2767230135693902128766236987544547378777436388091785064756910, 689644486314086496286093830416975206144754872092432108597436, 138642086125227682870831666630271950088954885603515871632201, 30047434693445231347602467117028303851832764185641774643468, 6851801387424175873694354145711254327404855789285230103013, 2120042874205307146695207067554609162977513984517631857617, 490320105846897857421254356104910632681008002313418940471, 126323731373804665276167034060996983366300068355660603173, 21699921539905324453875345006818945922412432384306278913, 7939681050823987735942326816454304705408373515598927024, 1704054406000164917101338955641076586996654015897777293, 674629720702507360892410918497513853241707768110535720, 130116804903893330957629746403630277914984408897684191, 36586674897705341032938585410676119549859764313014514, 6820517853488553816157069373430435510514248629408934, 1940615831245060580576779381334292194461763717429719, 486407487540373443078130965659847688641455681092783, 115503902548715291215146001384729209189201342203617, 20726453501406140054607926221786392225949497849620, 5795586010156766459954451266198423523738902544440, 1894126095992857664160110316211206136427948391401, 400235284644456465531456917507977101554184036138, 96821039379669584765064498053975819680674844391, 23003305579401059533778299981921977893360385917, 5228073966664279351555893540080524011514115962, 1242198234479925081489833339665036257581784830, 412185918978837707936146917867270887000813745, 100133634343775138722999743130814482251294603, 26059544917887755330857182088221243972088111, 5139528748995372887990321340679356174733638, 1253542354308041615766358708614160342158058, 255695244303425264981809526736239333102982, 61808370933695923699986081041674755242751, 12426096507290278206573602748929564597975, 2986453750810080523307169404271220297061, 642144302488057714162005557670195083334, 130361391592026886001154254666792730817, 38722902212652057786773086799878934378, 7692285091800305362911294817569041066, 2668441901840977427307689562983863761, 627879703191450992712744583653335581, 143466848278452388635765854137055267, 40114449315047293082657646359855538, 9604649217508319090540717981276261, 2160954625898663094838587676686854, 663518655289550974870054172122371, 165231181091826810616798470843406, 32017505733146837917121936265672, 6710170503572414769550988030906, 2193907060628154300461720427652, 655138594818423378286082953437, 128372286376670762441323321515, 34081674525017606572942142473, 9410152783640368288366142632, 2828735859241558188208098320, 551007171562149788272788426, 123790351812017402954987183, 26171709615346256252881994, 5974406115827778237616062, 1129305631130982975444977, 309305180419035303006618, 63076647774929269450546, 17802308053095636943505, 5708739899619810440888, 1717642617243788103954, 487452007321104273269, 128040514304008259695, 22395338754966061650, 6980614247696882509, 1954726203330249242, 521378690601084559, 136837526017031961, 29173740577404415, 7191768065683254, 1621292657659019, 549037231011822, 141224784287699, 28266584508619, 8568210839573, 1730361037440, 343914088335, 79692432578, 29986725790, 6384194185, 1319027283, 483793159, 103505140, 22103086, 7280487, 2401760, 411716, 143073, 37097, 10436, 1884, 649, 134, 40, 14, 3, 1]
c = 2488656295807929935404316556194747314175977860755594014838879551525915558042003735363919054632036359039039831854134957725034750353847782168033537523854288427613513938991943920607437000388885418821419115067060003426834

m = ''

for i in a:
    if i > c:
        m += '0'
    else:
        c -= i
        m += '1'

m_bin = eval('0b'+m)
print(long_to_bytes(m_bin).decode())  # BaseCTF{2c4b0c15-3bee-4e4a-be6e-0f21e44bd4c9}

【flag】

1	BaseCTF{2c4b0c15-3bee-4e4a-be6e-0f21e44bd4c9}

========================================================================================

babyrsa

from Crypto.Util.number import *

flag=b'BaseCTF{}'
m=bytes_to_long(flag)

n=getPrime(1024)
e=65537
c=pow(m,e,n)

print("n =",n)
print("e =",e)
print("c =",c)
"""
n = 104183228088542215832586853960545770129432455017084922666863784677429101830081296092160577385504119992684465370064078111180392569428724567004127219404823572026223436862745730173139986492602477713885542326870467400963852118869315846751389455454901156056052615838896369328997848311481063843872424140860836988323
e = 65537
c = 82196463059676486575535008370915456813185183463924294571176174789532397479953946434034716719910791511862636560490018194366403813871056990901867869218620209108897605739690399997114809024111921392073218916312505618204406951839504667533298180440796183056408632017397568390899568498216649685642586091862054119832
"""

考点：欧拉函数
解析

其中有n=getPrime(1024)，素数的欧拉函数是它减一（因为它与小于它所有的数都互为素数），得到phi就可以求d，并不用求p和q。接下来就和正常解rsa就行

from Crypto.Util.number import *

n = 104183228088542215832586853960545770129432455017084922666863784677429101830081296092160577385504119992684465370064078111180392569428724567004127219404823572026223436862745730173139986492602477713885542326870467400963852118869315846751389455454901156056052615838896369328997848311481063843872424140860836988323
e = 65537
c = 82196463059676486575535008370915456813185183463924294571176174789532397479953946434034716719910791511862636560490018194366403813871056990901867869218620209108897605739690399997114809024111921392073218916312505618204406951839504667533298180440796183056408632017397568390899568498216649685642586091862054119832

d = inverse(e, n-1)
m = pow(c, d, n)
print(long_to_bytes(m).decode()) # BaseCTF{7d7c90ae-1127-4170-9e0d-d796efcd305b}

【flag】

1	BaseCTF{7d7c90ae-1127-4170-9e0d-d796efcd305b}

========================================================================================

ez_math

【感觉】：矩阵，不会

【task.py】

import numpy as np
from Crypto.Util.number import *

a, b, c, d = [getPrime(128) for _ in range(4)]
point1 = a * d
point2 = b * c
matrix2 = [[0, a, b], [0, c, d]]

flag = b"flag{test_flag}"
flag = bytes_to_long(flag)


def randomArray():
    upper = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
    low = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
    for i in range(3):
        for j in range(i+1, 3):
            upper[i][j] = getPrime(128)
            low[j][i] = getPrime(128)
    result = np.array(upper) @ np.array(low)   # 两个数组之间相加
    return result

A = np.array([[flag, 0, 0]] + matrix2)  # 每一行第一个都加上了flag
B = randomArray()
MAT = A @ B

print(point1)
print(point2)
print(MAT)

'''
85763755029292607594055805804755756282473763031524911851356658672180185707477
70470862191594893036733540494554536608294230603070251013536189798304544579643
[[73595299897883318809385485549070133693240974831930302408429664709375267345973630251242462442287906226820558620868020093702204534513147710406187365838820773200509683489479230005270823245
  46106113894293637419638880781044700751458754728940339402825975283562443072980134956975133603010158365617690455079648357103963721564427583836974868790823082218575195867647267322046726830
  161159443444728507357705839523372181165265338895748546250868368998015829266587881868060439602487400399254839839711192069105943123376622497847079185]
 [13874395612510317401724273626815493897470313869776776437748145979913315379889260408106588331541371806148807844847909
  17025249852164087827929313934411832021160463738288565876371918871371314930048841650464137478757581505369909723030523
  59510107422473463833740668736202898422777415868238817665123293560097821015330]
 [11314088133820151155755028207579196628679021106024798818326096960197933616112389017957501267749946871903275867785729
  13883500421020573457778249958402264688539607625195400103961001780695107955462968883861677871644577542226749179056659
  48528427402189936709203219516777784993195743269405968907408051071264464132448]]
'''

【解析】

百度了一下——“三角矩阵的行列式就是其对角线上元素的乘积”

结合[BaseCTF2024]sudopacman个人Writeup

三角形行列式_百度百科 (baidu.com)是一种特殊的行列式，包括上三角形行列式和下三角形行列式，亦称上三角行列式和下三角行列式，统称三角形行列式。,每个行列式都可以只运用行或者列的性质化为一个与其相等的上 (下)三角形行列式，上 (或下)三角形行列式都等于它们主对角线上元素的乘积 [1]。)

python:@运算符（numpy库中的运算符）-CSDN博客食用

randomArray()函数生成了两个

1 2	对角线为1 上半部分由随机数`getPrime(128)`填充的上三角矩阵对角线为1 下半部分由随机数`getPrime(128)`填充的下三角矩阵

然后进行矩阵乘法 @，对这个符号不熟可以看第三篇文章

那么按照前文铺垫，B的行列式就是对角线乘积，也就是1

那么$MAT = A$

已给出A矩阵 (对于为什么会是这个后面会说)

$\begin{bmatrix} flag & 0 & 0 \\ 0 & a & b \\ 0 & c & d \end{bmatrix}$

的分块矩阵

$\begin{bmatrix} a & b \\ c & d \end{bmatrix}$

后者的行列式为$a\cdot d-b \cdot c$ ，其中$a\cdot d$就为point1，$b\cdot c$就为point2，那么A的行列式为

$|A| = |flag|\cdot(point1-point2)$

即$MAT$的行列式整除(point1-point2)即可得到flag

对于为什么A矩阵的形式，本人原因，并未接触到矩阵的系统学习，在网上搜了个大概，在这里说一下自己的理解一下，多多包含

——因为相当于先把含有flag的矩阵垫高了变成3x3方形矩阵（下图一），并把含有abcd的矩阵拉低变成3x3的方形矩阵（下图二），然后再相加，所以得到上图A矩阵的样子。

$\begin{bmatrix} flag & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$ $\begin{bmatrix} 0 & 0 & 0 \\ 0 & a & b \\ 0 & c & d \end{bmatrix}$

【EXP】

# sagemath
from Crypto.Util.number import *
point1 = 85763755029292607594055805804755756282473763031524911851356658672180185707477
point2 = 70470862191594893036733540494554536608294230603070251013536189798304544579643

MAT = [
    [73595299897883318809385485549070133693240974831930302408429664709375267345973630251242462442287906226820558620868020093702204534513147710406187365838820773200509683489479230005270823245,
  46106113894293637419638880781044700751458754728940339402825975283562443072980134956975133603010158365617690455079648357103963721564427583836974868790823082218575195867647267322046726830,
  161159443444728507357705839523372181165265338895748546250868368998015829266587881868060439602487400399254839839711192069105943123376622497847079185],
 [13874395612510317401724273626815493897470313869776776437748145979913315379889260408106588331541371806148807844847909,
  17025249852164087827929313934411832021160463738288565876371918871371314930048841650464137478757581505369909723030523,
  59510107422473463833740668736202898422777415868238817665123293560097821015330],
 [11314088133820151155755028207579196628679021106024798818326096960197933616112389017957501267749946871903275867785729,
  13883500421020573457778249958402264688539607625195400103961001780695107955462968883861677871644577542226749179056659,
  48528427402189936709203219516777784993195743269405968907408051071264464132448]
  ]

m = det(Matrix(MAT)) // (point1 - point2)
flag = long_to_bytes(m).decode()
print(flag)

flag

1	BaseCTF{7E9328AF-784C-8AF5-AC10-D6A8FC0977A8}

========================================================================================

mid_math

【感觉】：先复现上面baby_math再说看看复现的怎么样

学成归来

套上面那个EXP就行

【flag】

1	BaseCTF{E439646E-1768-18B3-DC4B-483C40C5340C}

========================================================================================

ez_rsa

【感觉】：给了no_phi，括号展开减去n就有了p+q，放到phi公式即可算出

【task.py】

from Crypto.Util.number import *
import gmpy2
m=bytes_to_long(b'BaseCTF{th1s_is_fake_fl4g}')
e=65537
p=getPrime(512)
q=getPrime(512)
n=p*q
not_phi=(p+2)*(q+2)
c=pow(m,e,n)

print(n)
print(not_phi)
print(c)


'''
96557532552764825748472768984579682122986562613246880628804186193992067825769559200526147636851266716823209928173635593695093547063827866240583007222790344897976690691139671461342896437428086142262969360560293350630096355947291129943172939923835317907954465556018515239228081131167407674558849860647237317421
96557532552764825748472768984579682122986562613246880628804186193992067825769559200526147636851266716823209928173635593695093547063827866240583007222790384900615665394180812810697286554008262030049280213663390855887077502992804805794388166197820395507600028816810471093163466639673142482751115353389655533205
37077223015399348092851894372646658604740267343644217689655405286963638119001805842457783136228509659145024536105346167019011411567936952592106648947994192469223516127472421779354488529147931251709280386948262922098480060585438392212246591935850115718989480740299246709231437138646467532794139869741318202945
'''

【解析】

从no_phi中提取$p+q$ ，$phi = (p-1)\cdot (q-1)=n-(p+q)+1$

【EXP】

# 创物者：善嵯峨
# 创物时间：2024/11/25 21:01
from Crypto.Util.number import *

n = 96557532552764825748472768984579682122986562613246880628804186193992067825769559200526147636851266716823209928173635593695093547063827866240583007222790344897976690691139671461342896437428086142262969360560293350630096355947291129943172939923835317907954465556018515239228081131167407674558849860647237317421
no_phi = 96557532552764825748472768984579682122986562613246880628804186193992067825769559200526147636851266716823209928173635593695093547063827866240583007222790384900615665394180812810697286554008262030049280213663390855887077502992804805794388166197820395507600028816810471093163466639673142482751115353389655533205
c = 37077223015399348092851894372646658604740267343644217689655405286963638119001805842457783136228509659145024536105346167019011411567936952592106648947994192469223516127472421779354488529147931251709280386948262922098480060585438392212246591935850115718989480740299246709231437138646467532794139869741318202945
e = 65537

pq = (no_phi - n - 4) // 2

phi = n - pq + 1
d = inverse(e, phi)

m = pow(c, d, n)
print(long_to_bytes(m).decode())

【flag】

1	BaseCTF{it_1s_ez!!}

========================================================================================

helloCrypto

【感觉】：AES，给了key和密文，拿去给AI写脚本，或者自己用pycryptodome库来做

【EXP】

from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad

# 已知的密钥整数值
key_int = 208797759953288399620324890930572736628
# 将整数值转换回16字节的密钥
key = long_to_bytes(key_int)

# 已知的密文
ciphertext = b'U\xcd\xf3\xb1 r\xa1\x8e\x88\x92Sf\x8a`Sk],\xa3(i\xcd\x11\xd0D\x1edd\x16[&\x92@^\xfc\xa9(\xee\xfd\xfb\x07\x7f:\x9b\x88\xfe{\xae'

# 创建AES解密对象
aes_decrypt = AES.new(key=key, mode=AES.MODE_ECB)

# 解密密文
decrypted_data = aes_decrypt.decrypt(ciphertext)

# 移除填充
flag = unpad(decrypted_data, AES.block_size)

print(flag)

【flag】

1	BaseCTF{b80bf679-1869-4fde-b3f9-d51b872d31fb}

========================================================================================

你会算md5吗

【想法】：逐字节爆破md5，然后比较，或许可以先建一个字典，然后取值。

【题目】

import hashlib

flag='BaseCTF{}'

output=[]
for i in flag:
    my_md5=hashlib.md5()
    my_md5.update(i.encode())
    output.append(my_md5.hexdigest())
print("output =",output)
'''
output = ['9d5ed678fe57bcca610140957afab571', '0cc175b9c0f1b6a831c399e269772661', '03c7c0ace395d80182db07ae2c30f034', 'e1671797c52e15f763380b45e841ec32', '0d61f8370cad1d412f80b84d143e1257', 'b9ece18c950afbfa6b0fdbfa4ff731d3', '800618943025315f869e4e1f09471012', 'f95b70fdc3088560732a5ac135644506', '0cc175b9c0f1b6a831c399e269772661', 'a87ff679a2f3e71d9181a67b7542122c', '92eb5ffee6ae2fec3ad71c777531578f', '8fa14cdd754f91cc6554c9e71929cce7', 'a87ff679a2f3e71d9181a67b7542122c', 'eccbc87e4b5ce2fe28308fd9f2a7baf3', '0cc175b9c0f1b6a831c399e269772661', 'e4da3b7fbbce2345d7772b0674a318d5', '336d5ebc5436534e61d16e63ddfca327', 'eccbc87e4b5ce2fe28308fd9f2a7baf3', '8fa14cdd754f91cc6554c9e71929cce7', '8fa14cdd754f91cc6554c9e71929cce7', '45c48cce2e2d7fbdea1afc51c7c6ad26', '336d5ebc5436534e61d16e63ddfca327', 'a87ff679a2f3e71d9181a67b7542122c', '8f14e45fceea167a5a36dedd4bea2543', '1679091c5a880faf6fb5e6087eb1b2dc', 'a87ff679a2f3e71d9181a67b7542122c', '336d5ebc5436534e61d16e63ddfca327', '92eb5ffee6ae2fec3ad71c777531578f', '8277e0910d750195b448797616e091ad', '0cc175b9c0f1b6a831c399e269772661', 'c81e728d9d4c2f636f067f89cc14862c', '336d5ebc5436534e61d16e63ddfca327', '0cc175b9c0f1b6a831c399e269772661', '8fa14cdd754f91cc6554c9e71929cce7', 'c9f0f895fb98ab9159f51fd0297e236d', 'e1671797c52e15f763380b45e841ec32', 'e1671797c52e15f763380b45e841ec32', 'a87ff679a2f3e71d9181a67b7542122c', '8277e0910d750195b448797616e091ad', '92eb5ffee6ae2fec3ad71c777531578f', '45c48cce2e2d7fbdea1afc51c7c6ad26', '0cc175b9c0f1b6a831c399e269772661', 'c9f0f895fb98ab9159f51fd0297e236d', '0cc175b9c0f1b6a831c399e269772661', 'cbb184dd8e05c9709e5dcaedaa0495cf']
'''

【解析】

分析脚本，for i in flag: 逐个字母计算md5，那么很好反推

【EXP】

import hashlib
import string


# 计算字符串的MD5值
def calculate_md5(s):
    return hashlib.md5(s.encode()).hexdigest()

# 字母集合，包括下划线和花括号
letters = string.printable

# 创建一个字典来存储字母和它们的MD5值
md5_dict = {calculate_md5(letter): letter for letter in letters}

# 给定的MD5值数组
md5_array = ['9d5ed678fe57bcca610140957afab571', '0cc175b9c0f1b6a831c399e269772661', '03c7c0ace395d80182db07ae2c30f034', 'e1671797c52e15f763380b45e841ec32', '0d61f8370cad1d412f80b84d143e1257', 'b9ece18c950afbfa6b0fdbfa4ff731d3', '800618943025315f869e4e1f09471012', 'f95b70fdc3088560732a5ac135644506', '0cc175b9c0f1b6a831c399e269772661', 'a87ff679a2f3e71d9181a67b7542122c', '92eb5ffee6ae2fec3ad71c777531578f', '8fa14cdd754f91cc6554c9e71929cce7', 'a87ff679a2f3e71d9181a67b7542122c', 'eccbc87e4b5ce2fe28308fd9f2a7baf3', '0cc175b9c0f1b6a831c399e269772661', 'e4da3b7fbbce2345d7772b0674a318d5', '336d5ebc5436534e61d16e63ddfca327', 'eccbc87e4b5ce2fe28308fd9f2a7baf3', '8fa14cdd754f91cc6554c9e71929cce7', '8fa14cdd754f91cc6554c9e71929cce7', '45c48cce2e2d7fbdea1afc51c7c6ad26', '336d5ebc5436534e61d16e63ddfca327', 'a87ff679a2f3e71d9181a67b7542122c', '8f14e45fceea167a5a36dedd4bea2543', '1679091c5a880faf6fb5e6087eb1b2dc', 'a87ff679a2f3e71d9181a67b7542122c', '336d5ebc5436534e61d16e63ddfca327', '92eb5ffee6ae2fec3ad71c777531578f', '8277e0910d750195b448797616e091ad', '0cc175b9c0f1b6a831c399e269772661', 'c81e728d9d4c2f636f067f89cc14862c', '336d5ebc5436534e61d16e63ddfca327', '0cc175b9c0f1b6a831c399e269772661', '8fa14cdd754f91cc6554c9e71929cce7', 'c9f0f895fb98ab9159f51fd0297e236d', 'e1671797c52e15f763380b45e841ec32', 'e1671797c52e15f763380b45e841ec32', 'a87ff679a2f3e71d9181a67b7542122c', '8277e0910d750195b448797616e091ad', '92eb5ffee6ae2fec3ad71c777531578f', '45c48cce2e2d7fbdea1afc51c7c6ad26', '0cc175b9c0f1b6a831c399e269772661', 'c9f0f895fb98ab9159f51fd0297e236d', '0cc175b9c0f1b6a831c399e269772661', 'cbb184dd8e05c9709e5dcaedaa0495cf']  # 替换为实际的MD5值列表

# 用于存储匹配字母的变量
flag = ''

# 比较MD5值并更新flag变量
for md5_value in md5_array:
    if md5_value in md5_dict:
        flag += md5_dict[md5_value]


# 输出结果
print(f"匹配的字母集合: {flag}")

让ai生成一个脚本的时候犯了个错误，应该是md5值做字典的键，然后对应字母做值，这样后续查找才方便找。

然后给的字母范围也错了，用string.printable就行了

【flag】

1	BaseCTF{a4bf43a5-3ff9-4764-bda2-af8ee4db9a8a}

========================================================================================

week2

basic

题目

from Crypto.Util.number import *
import socketserver
import os
import random
import base64
import string

flag = os.getenv('GZCTF_FLAG').encode()


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self):
        return self._recvall()
    
    def handle(self):
        printable_chars = string.ascii_letters + string.digits + string.punctuation
        optional=[b'A',b'B',b'C',b'D']
        for _ in range(100):
            secret= ''.join(random.choices(printable_chars, k=16)).encode()
            select=random.choice(optional)
            self.send(select)
            enc=b''
            if select==b'A':
                enc=base64.b64encode(secret)
            elif select==b'B':
                enc=secret.hex().encode()
            elif select==b'C':
                enc=bytes_to_long(secret)
                enc=str(enc).encode()
            elif select==b'D':
                enc=[i for i in secret]
                enc=str(enc).encode()
            self.send(enc)
            client_send=self.recv()
            if client_send!=secret:
                self.send("\nYou wrong!!!!!")
                exit()

        self.send(flag)
        self.send(b"\nConnection has been closed  =.=  ")
        self.request.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 9999
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

解析

给ai分析一下这代码，得知是有四种加密方式，每次随机用一种方式来加密随机生成的字符串，告诉你加密方式和密文，让你输入解密后的明文，重复一百遍后便出flag，这题旨在考查使用pwntools库来连接，和处理字符串和字节串（用.decode或者截取然后用ord()转字符）。有耐心的老哥也可以写一个代码，用人工充当pwntools，一边python解密，一边ncat终端连接交互。

人工组手搓版（用来一遍遍调试，看看解密方式和输入到终端的字符格式是否正确）

for i in range(101):
    select = input()
    if select == 'a':
        # A
        import base64

        enc = input()
        m = base64.b64decode(enc).decode()
        print('A:', m)


    elif select == 'b':
        # B

        enc = input()
        m = bytes.fromhex(str(enc)).decode()
        print("B:", m)

    elif select == 'c':
        # C
        from Crypto.Util.number import *
        enc = int(input())
        m = long_to_bytes(enc).decode()
        print('C:', m)

    elif select == 'd':
        # D
        enc = eval(input())
        m = ""
        for i in enc:
            m += chr(i)
        print('D:', m)

机械组 pwntools

from pwn import *
context(arch = 'i386', os = 'linux')


io = remote("challenge.basectf.fun", 38254)

for i in range(101):
    select = io.recvline()   # 或者直接 select = io.recvline().strip().decode() 可以替换下面的select = chr(select[0])
    print(select)
    select = chr(select[0])
    print(select)
    print(select == 'A' or select == 'B' or select == 'C' or select == 'D')
    if select == 'A':
        # A
        import base64

        enc = io.recvline().decode()
        m = base64.b64decode(enc).decode()
        io.send(m)


    elif select == 'B':
        # B

        enc = io.recvline().decode()
        m = bytes.fromhex(str(enc)).decode()
        io.send(m)

    elif select == 'C':
        # C
        from Crypto.Util.number import *
        enc = int(io.recvline())
        m = long_to_bytes(enc).decode()
        io.send(m)

    elif select == 'D':
        # D
        enc = eval(io.recvline())
        m = ""
        for i in enc:
            m += chr(i)
        io.send(m)

【flag】

1	BaseCTF{1732e054-e172-4d94-b5cf-3fb7bb022091}

========================================================================================

two_squares

题目

from Crypto.Util.number import *
flag=b'BaseCTF{}'
m=bytes_to_long(flag)
p=getPrime(128)
q=getPrime(128)
n=p*q
e=65537
c=pow(m,e,n)
x=p^2+q^2
print("e =",e)
print("c =",c)
print("x =",x)

"""
e = 65537
c = 42330675787206041757903427737108553993012805007294570657461042152628982126538
x = 209479773119142584969854470862023704936857416491817498021871883305658177375498
"""

分析

小整数快速分解为平方和的函数

10版本

学习网址Fast decomposition of small integers into sums of squares - Standard Commutative Rings (sagemath.org)

分解为四个平方和

1	four_squares_pyx()

分解为三个平方和

1	three_squares_pyx()

分解为二个平方和

1	two_squares_pyx()

判断一个数是否为两个数平方和

1 2	[x for x in range(30) if is_sum_of_two_squares_pyx(x)] [0, 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 18, 20, 25, 26, 29]

#sagemath 9.3

from Crypto.Util.number import *
e = 65537
c = 42330675787206041757903427737108553993012805007294570657461042152628982126538
x = 209479773119142584969854470862023704936857416491817498021871883305658177375498

p,q = two_squares(x)
n = p*q
phi = (p-1)*(q-1)
d = inverse(e,phi)
m = pow(c,d,n)

flag = long_to_bytes(int(m))
print(flag) # BaseCTF{0760becd-cefaab0b094d}

【flag】

1	BaseCTF{0760becd-cefaab0b094d}

========================================================================================

铜匠

题目

from Crypto.Util.number import getPrime, bytes_to_long
#from secret import flag
flag=b'XXXX'

p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 721
hint2 = q % (2 ** 266)
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)
'''
hint1 = 14439249591349619691972392177790365247490839237199085979433418493254022567815148979672690178
hint2 = 90063199151369157959005663017593053931871580139169245885113098598755909124764417
n = 18347545778876678838092757800261556931131930866012101566000425608407193858675622059415995283684230959320874387944052648148677918542763633503231962873204645415818139345588988936580526094727943067102768943117592654029397879665312089518191052154267343886226820785206334238961064175118262578895847281575656290248049404047727756356910896332939145136942219317065063060070725033146788186604738271846183709127655298440696824683099637827282095133642324657860714680107691622056420045091586609974536644773286992447027164350612852922016376888380895187804771279035652496676089183636450028327097084911908336202253562671798012457461
ct = 15659576879410368237140555530527974801613150473447768911067611094143466009251385693099110691602954207905029692682380253595062935017486879899242785756448973466690818942065250284891341066578689696180061755610538867770441139827574063212967027249650509215685566103350688284041405586915563454117672061141919712416360596137520514412607512596079964611672166435592936417138352662031529414118312166411150736015788925026636845744110093161894267707446937939130745326244186579516665160036229715964182962542836836457885170975474737620430886449029488829662146456489724775166105816909257516908496172172266375617868819982791477888289
'''

解析

在查small_root()参数要求时，找到了原题鹤城杯2021，babyrsa

文章RSA中coppersmith定理的应用条件_sagemath coppersmith-CSDN博客

测试一下在pq均为1024位下，未知量需要控制在多少一下才能使得small_root()有解

from Crypto.Util.number import getPrime
p = getPrime(int(1024)) # 1024可根据题意修改，若p，q不同位，请访问https://blog.csdn.net/qq_51999772/article/details/123620932
q = getPrime(int(1024))
n = p * q
test_bits = 455 # 调节未知数大小
p_h = p >> test_bits
R.<x> = PolynomialRing(Zmod(n))
f = (p_h << test_bits) + x
f.small_roots(2**test_bits,0.4)

# sagemath 9.3
from Crypto.Util.number import *
hint1 = 14439249591349619691972392177790365247490839237199085979433418493254022567815148979672690178
hint2 = 90063199151369157959005663017593053931871580139169245885113098598755909124764417
n = 18347545778876678838092757800261556931131930866012101566000425608407193858675622059415995283684230959320874387944052648148677918542763633503231962873204645415818139345588988936580526094727943067102768943117592654029397879665312089518191052154267343886226820785206334238961064175118262578895847281575656290248049404047727756356910896332939145136942219317065063060070725033146788186604738271846183709127655298440696824683099637827282095133642324657860714680107691622056420045091586609974536644773286992447027164350612852922016376888380895187804771279035652496676089183636450028327097084911908336202253562671798012457461
ct = 15659576879410368237140555530527974801613150473447768911067611094143466009251385693099110691602954207905029692682380253595062935017486879899242785756448973466690818942065250284891341066578689696180061755610538867770441139827574063212967027249650509215685566103350688284041405586915563454117672061141919712416360596137520514412607512596079964611672166435592936417138352662031529414118312166411150736015788925026636845744110093161894267707446937939130745326244186579516665160036229715964182962542836836457885170975474737620430886449029488829662146456489724775166105816909257516908496172172266375617868819982791477888289
e = 65537

p_high = hint1
q_low = hint2
mod = 2 ** 266
q_low_lnv = inverse(q_low, mod)
p_low = n*q_low_lnv % mod

i = 721 - 266 - 455 # i是p距离small_root成功所需要的位数还缺的位数（用来爆破），455是用另一个py文件推出来的
print(i)
PR.<x> = PolynomialRing(Zmod(n))
if i != 0:
    for j in range(2**i):
        f = p_high * (2**721) + p_low + (x*32  + j) * mod # 这里的32是步长
        f = f.monic()
        out_p = f.small_root(2**455,0.4)
        if(len(out_p) != 0): 
            print(out_p)
            break
    p = (out_p[0]*32 + j) * mod + p_high * (2**721) + p_low

else:
    f = p_high * (2**721) + p_low + (x*32) * 2**266
    f = f.monic()
    out_p = f.small_roots(2**455,0.4)
    p = p_high * (2**721) + p_low + (out_p[0]*32) * 2**266
    


p = int(p)
assert n%p == 0
q = n//p
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(ct, d, n)
flag = long_to_bytes(int(m))
print(flag.decode()) # BaseCTF{7074ddc3e006810688241196414e49e2}

【flag】

1	BaseCTF{7074ddc3e006810688241196414e49e2}

========================================================================================

random_primes

题目

from Crypto.Util.number import *
import random
def gen_n():
    primes=[getPrime(128) for _ in range(256)]
    n = 1
    for i in range(100):
        n *= primes[random.randint(0,127)]
    return primes,n

flag=b'BaseCTF{}'
m=bytes_to_long(flag)

assert len(flag)==45

primes,n = gen_n()
e = 0x010001

c=pow(m,e,n)

print("n =",n)
print("e =",e)
print("c =",c)
print("primes =",primes)

分析

给了flag长度45，写个脚本看flag位数（二进制）

from Crypto.Util.number import *
flag0 = b'BaseCTF{'
i = 0
flag = flag0 + b'a'*i + b'}' 


while len(flag) < 45:    # 45可改，根据题目修改
    i += 1
    flag = flag0 + b'a'*i + b'}'
print(i)
m = bytes_to_long(flag)
print(m.bit_length()) # 359

是359位，每个素数都是128位，拿三个素数就有128*3=384位，远大于359位。所以可以拿这三个素数来模整体，看看rsa解出来，记得把n也给换了

from Crypto.Util.number import *

n = 
e = 65537
c = 
primes = []

for i in primes:
    for j in primes[2:]:
        for k in primes[3:]:
            n = i*j*k             # 记得换n
            phi = (i-1)*(j-1)*(k-1)
            d = inverse(e, phi)
            m = pow(c, d, n)
            flag = long_to_bytes(m)
            if b'BaseCTF' in flag:
                print(flag.decode())
                exit()

【flag】

1	BaseCTF{7cf4eedb-8b2d-406f-83bf-b2cb70882832}

========================================================================================

mid_math2

【想法】：已经给了n的三个因子，就是MAT第一行的那三个

import numpy as np
from Crypto.Util.number import *

a, b, c = [getPrime(128) for _ in range(3)]
d, e, f, h, i, j = [getPrime(1024) for _ in range(6)]
A = [[a, b, c], [d, e, f], [h, i, j]]

flag = b"flag{test_flag}"
flag = bytes_to_long(flag)

def prod(myList):
    result = 1
    for i in myList:
        result = result * i
    return result

def randomArray():
    upper = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
    low = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
    for i in range(3):
        for j in range(i+1, 3):
            upper[i][j] = getPrime(128)
            low[j][i] = getPrime(128)
    result = np.array(upper) @ np.array(low)
    return result

e = getPrime(18)
N = getPrime(1024)
C = randomArray()
#MAT = C @ A @ B
MAT = C @ A
c = pow(flag, e, prod(A[0]))

print(MAT)
print(f'c = {c}')
print(f'e = {e}')

'''
[[9194428734244577957135736828947112370812209206819996917633266069359894211949655026549592464237531352518967649750275097282532736237822915630766535634248987628113137246739472264614337707439494149796414126558156060870508338278038269649101921703583149322486905552569052814106532234864028314925118581658029792157851338427975728108000711353532410024128431635933014226306706319591106081211872
  7052600738698435126221697697810087514520765619736355003187836563546493264420232197860875416948961661231812045406188307561458872254314061097960625042149316957446344556490001927621879295417925720004568332344856366002394724202261454916368122811414228043610804718983599804179657247820737462743875143882925818085495573474169110616761320858675303922740882169073395416895304752909979711051264
  13094262565727554986668133240216117564284263232131011542877585146452802164148464500319291219458081531317231044962383872061004846788004747813785963603455919882739054992075130196548494850105124430477756818974520035883861936342117869122455996838023977818945511119955390136020375974150407580576040034808588694313922810340598787633148909527275716235390356737099830131958338026891256778602432]
 [7291452286171544741377496447735677778433522048452394999757158120018504601116506253897733192493798837108269469756414516913436198353934250444263790689101779479157541198872731006007031448329354826004420971505929629537584453480285628607579031078497417101681028600589030661495031531644755072500393418929237208836713910921969937998825721580514845395852889662758886414966066733340052235985735
  5592919719754926663830816961667268104316637431189640788304536404157195458040686322901848820171568258023938724485177544141303597034389473064509506247034833050568643394732003598890104462382321956436508366359718039669456303596542945687737870352569084995858128262046585579724537002100295978230177579835256681774512205534970583421138287684468047290246482431883957170924203400422234299829407
  10384135162743100269852365857770153822630076412853981379757028821332622753962517667857057209221058533163475030678127399042436975886694593504673386134198042731671320468065688239424934644173240507619471360908786669070898288638067852779718549009532013299792474712979659423962779677856135791013599792822988457540442172903145046394648862567656330868441373023488569784114231877910285319620037]
 [34946383530632295853235791100380055176686898072752599942691162027311662041417740482507624946631032260410440329949488242706004902881977357811370156793240362927747354453547446315050117795844866771053429455608334265986953931753411938119703800489233043034369650346216548318254326462336573090313788936967898128977445514764945671848611612198443909056919
  26805677375585831510259621878357023272222175103906204143689109861471123435549853025410319713500257027420994041712736040084303902812241806295302385126726161281240831030434347236854521776375408982352155894199700974681768432734155312616453345950508256035721377179651166114898547487082749355033867559583905997404388549346221139007108462958001461826337
  49768956277664050500387501949373949828589012443212214016088015478826178759698946452495063308332332373728223252613132611904477061717762261927498754849913008747980442098787524359755695519989286304445175440218168145037681791003471134417445542856715034633656861298596197935068562189476201463465706711744838395255326376049859058504891392128431832044455]]
c = 11781599055433308033432930805524658061560499523533841161297213162869735414528038973998414585008473948613388691447093
e = 160907
'''

【解析】

想法有点天真，可以自己验证一下，MAT的数与A是不同的，MAT每一位数明显比A要大。

这里有$|MAT|=|A|$ ，那么可以用LLL算法去找更好的基。

MAT = C @ A 是线性变换

LLL算法是线性变换

我也找不到MAT = C @ A矩阵乘法和 LLL算法之间有什么联系，除了都是线性变换

为什么能通过LLL算法找到MAT的最佳的基就是A矩阵

LLL算法进行的是 线性变换，它通过对原始基进行正交化和短化（即通过格的 Gram-Schmidt 正交化或其他类似步骤），但不改变格的体积。因此，虽然 A 是一个经过优化的基，它的行列式与原始的基是相同的。

https://jia.je/kb/cryptography/lll.html#_1

【EXP】

from Crypto.Util.number import *
MAT = [[9194428734244577957135736828947112370812209206819996917633266069359894211949655026549592464237531352518967649750275097282532736237822915630766535634248987628113137246739472264614337707439494149796414126558156060870508338278038269649101921703583149322486905552569052814106532234864028314925118581658029792157851338427975728108000711353532410024128431635933014226306706319591106081211872,
  7052600738698435126221697697810087514520765619736355003187836563546493264420232197860875416948961661231812045406188307561458872254314061097960625042149316957446344556490001927621879295417925720004568332344856366002394724202261454916368122811414228043610804718983599804179657247820737462743875143882925818085495573474169110616761320858675303922740882169073395416895304752909979711051264,
  13094262565727554986668133240216117564284263232131011542877585146452802164148464500319291219458081531317231044962383872061004846788004747813785963603455919882739054992075130196548494850105124430477756818974520035883861936342117869122455996838023977818945511119955390136020375974150407580576040034808588694313922810340598787633148909527275716235390356737099830131958338026891256778602432],
 [7291452286171544741377496447735677778433522048452394999757158120018504601116506253897733192493798837108269469756414516913436198353934250444263790689101779479157541198872731006007031448329354826004420971505929629537584453480285628607579031078497417101681028600589030661495031531644755072500393418929237208836713910921969937998825721580514845395852889662758886414966066733340052235985735,
  5592919719754926663830816961667268104316637431189640788304536404157195458040686322901848820171568258023938724485177544141303597034389473064509506247034833050568643394732003598890104462382321956436508366359718039669456303596542945687737870352569084995858128262046585579724537002100295978230177579835256681774512205534970583421138287684468047290246482431883957170924203400422234299829407,
  10384135162743100269852365857770153822630076412853981379757028821332622753962517667857057209221058533163475030678127399042436975886694593504673386134198042731671320468065688239424934644173240507619471360908786669070898288638067852779718549009532013299792474712979659423962779677856135791013599792822988457540442172903145046394648862567656330868441373023488569784114231877910285319620037],
 [34946383530632295853235791100380055176686898072752599942691162027311662041417740482507624946631032260410440329949488242706004902881977357811370156793240362927747354453547446315050117795844866771053429455608334265986953931753411938119703800489233043034369650346216548318254326462336573090313788936967898128977445514764945671848611612198443909056919,
  26805677375585831510259621878357023272222175103906204143689109861471123435549853025410319713500257027420994041712736040084303902812241806295302385126726161281240831030434347236854521776375408982352155894199700974681768432734155312616453345950508256035721377179651166114898547487082749355033867559583905997404388549346221139007108462958001461826337,
  49768956277664050500387501949373949828589012443212214016088015478826178759698946452495063308332332373728223252613132611904477061717762261927498754849913008747980442098787524359755695519989286304445175440218168145037681791003471134417445542856715034633656861298596197935068562189476201463465706711744838395255326376049859058504891392128431832044455]]
c = 11781599055433308033432930805524658061560499523533841161297213162869735414528038973998414585008473948613388691447093
e = 160907

MAT = Matrix(MAT)
A = MAT.LLL()
p, q, t = A[0]
p = abs(int(p))
q = abs(int(q))
t = abs(int(t))
n = p*q*t
phi = (p-1)*(q-1)*(t-1)
# print(phi)
d = inverse(e, phi)
m = pow(c, d, n)
flag = long_to_bytes(int(m)).decode()
print(flag)

【flag】

1	BaseCTF{8E2BD73F-9C10-F813-2CA4-B4B2DED4E961}

========================================================================================

try_to_factor

【想法】：原来生成的$gift_0$应该位数比N大，因为$gift_0$里面有最多6个偶数因子，最少有5个偶数因子，那么先还原再看看能否分解N

【题目】

from Crypto.Util.number import *
import random

flag = b'BaseCTF{}' + random.randbytes(64)
m = bytes_to_long(flag)

p, q, r, s, t = [getStrongPrime(512) for _ in range(5)]
N = p * q * r * s * t

n = p * q
e = 65537
c = pow(m, e, n)

gift = random.randint(2, n) * (p - 1) * (q - 1) * (r - 1) * (s - 1) * (t - 1)
while gift % 2 == 0:
    gift //= 2

print("N =", N)
print("c =", c)
print("gift =", gift)

"""
N = 162692163428762295773992659007654377270271126313772302197255271375236131917158614424426498628778734679898165422129699410934825650141972454562350664161510689489443251515884304101827584411577749250383438126881931889798597627663578045519256806107514170414321556291545302688028088470848270636776466672843710163017531472049823632822203461654253767303314505996071453898533003519236112138591066133289040889933161978131399309340741554076140734156174295730180874473301361701867633594222054688204666518058106672165786417002466165926062199279674267145233283545524775943767021416906072142236079753359492846480515376121887507681663761713445807717270089017438999615422884163666812016989696908657065537508715229685120221307021151610089917537155165897740417480127289719971512938348936259
c = 113962118676826667648935023618252851875440854724310328843964819392166304653581141146631375503931008732348730639629174670963727399860571217264854300057305570824097216782800531930906801885967717639795643406206813677461127762087560021634738167845077869308515223303820469892552545806179267969169748886980836435095
gift = 863514692222931709925579242743251211976114217396765747601042357918763818732391790491059528595917786523674732369068315533549380754409535403506339052401422249684188032949680148055803474336983973622610403448963752802490806614810077181934627694570685722842963961551889267501616799757825675192653489096007790143775773378495299981666657347802233798206597104474595281241837323214457344961462510183726339545608046357281265026013496037522835659867389206279894057481600882665189079672009577651494435000349624334685832217586703242422260870866432379257259316411280539845741932725104662417642890238587876489774492067722351467773093391502588019563488688309892102039611978767690653206664257400163618467825666105966072942726011447079204869750153256054140924951306811971422635104088608275908232688385437145325481792836532453258784103533536292492138405929815964841772656055397705840797739586953744563989819811944946916720655079908564653686456283647030055622241840292127096994325415897266379446446435164189216562921252341705747891518007710533906231225283309180960546212899099652226954393826875
"""

【解析】

从其中gift的构造可以看出，其因子至少有5个2（素数减一）

先乘上2^5，然后套脚本

如果分解不出那就再乘上2

【EXP】

from math import gcd
from math import isqrt
from random import randrange
from Crypto.Util.number import *

N = 162692163428762295773992659007654377270271126313772302197255271375236131917158614424426498628778734679898165422129699410934825650141972454562350664161510689489443251515884304101827584411577749250383438126881931889798597627663578045519256806107514170414321556291545302688028088470848270636776466672843710163017531472049823632822203461654253767303314505996071453898533003519236112138591066133289040889933161978131399309340741554076140734156174295730180874473301361701867633594222054688204666518058106672165786417002466165926062199279674267145233283545524775943767021416906072142236079753359492846480515376121887507681663761713445807717270089017438999615422884163666812016989696908657065537508715229685120221307021151610089917537155165897740417480127289719971512938348936259
c = 113962118676826667648935023618252851875440854724310328843964819392166304653581141146631375503931008732348730639629174670963727399860571217264854300057305570824097216782800531930906801885967717639795643406206813677461127762087560021634738167845077869308515223303820469892552545806179267969169748886980836435095
gift = 863514692222931709925579242743251211976114217396765747601042357918763818732391790491059528595917786523674732369068315533549380754409535403506339052401422249684188032949680148055803474336983973622610403448963752802490806614810077181934627694570685722842963961551889267501616799757825675192653489096007790143775773378495299981666657347802233798206597104474595281241837323214457344961462510183726339545608046357281265026013496037522835659867389206279894057481600882665189079672009577651494435000349624334685832217586703242422260870866432379257259316411280539845741932725104662417642890238587876489774492067722351467773093391502588019563488688309892102039611978767690653206664257400163618467825666105966072942726011447079204869750153256054140924951306811971422635104088608275908232688385437145325481792836532453258784103533536292492138405929815964841772656055397705840797739586953744563989819811944946916720655079908564653686456283647030055622241840292127096994325415897266379446446435164189216562921252341705747891518007710533906231225283309180960546212899099652226954393826875

phi1 = gift*2^5

def factorize(N, phi):
    """
    Recovers the prime factors from a modulus if Euler's totient is known.
    This method only works for a modulus consisting of 2 primes!
    :param N: the modulus
    :param phi: Euler's totient, the order of the multiplicative group modulo N
    :return: a tuple containing the prime factors, or None if the factors were not found
    """
    s = N + 1 - phi
    d = s ** 2 - 4 * N
    p = int(s - isqrt(d)) // 2
    q = int(s + isqrt(d)) // 2
    return p, q if p * q == N else None


def factorize_multi_prime(N, phi):
    """
    Recovers the prime factors from a modulus if Euler's totient is known.
    This method works for a modulus consisting of any number of primes, but is considerably be slower than factorize.
    More information: Hinek M. J., Low M. K., Teske E., "On Some Attacks on Multi-prime RSA" (Section 3)
    :param N: the modulus
    :param phi: Euler's totient, the order of the multiplicative group modulo N
    :return: a tuple containing the prime factors
    """
    prime_factors = set()
    factors = [N]
    while len(factors) > 0:
        # Element to factorize.
        N = factors[0]

        w = randrange(2, N - 1)
        i = 1
        while phi % (2 ** i) == 0:
            sqrt_1 = pow(w, phi // (2 ** i), N)
            if sqrt_1 > 1 and sqrt_1 != N - 1:
                # We can remove the element to factorize now, because we have a factorization.
                factors = factors[1:]

                p = gcd(N, sqrt_1 + 1)
                q = N // p

                if is_prime(p):
                    prime_factors.add(p)
                elif p > 1:
                    factors.append(p)

                if is_prime(q):
                    prime_factors.add(q)
                elif q > 1:
                    factors.append(q)

                # Continue in the outer loop
                break

            i += 1

    return tuple(prime_factors)




a = factorize_multi_prime(N, phi1)
print(len(a))

for i in a:
    for j in a:
        if i != j:
            phi = (i-1)*(j-1)
            n = i*j
            e = 65537
            
            d = inverse(e, phi)
            m = pow(c, d, n)
            if b"BaseCTF{" in long_to_bytes(m):
                print(long_to_bytes(m))

【flag】

1	BaseCTF{ed4bff90-d1f4-4f0f-a3bd-999c54d9eeb7}

========================================================================================

week3

exgcd

【想法】：给了两个e，加密同一个明文，用共模攻击

【题目】

from Crypto.Util.number import *

flag=b'BaseCTF{}'
m=bytes_to_long(flag)

p=getPrime(1024)
q=getPrime(1024)

n=p*q
e1=3747
e2=2991

c1=pow(m,e1,n)
c2=pow(m,e2,n)

print("n =",n)
print("e1 =",e1)
print("e2 =",e2)
print("c1 =",c1)
print("c2 =",c2)

"""
n = 27855350163093443890983002241607629119744539643165776358993469078731521668677421483556132628708836721737685936980427467856642738196111748018522018598646125626995613169001111504706363742194664774823604738939411512861441742683157275818500991834651769368178320088982759626122029956515159435424882855075032400667120376075618896752694718491438251810609878021717559466498493103257912108879328270813061231904227056671621363669388496383136964549879459562004569059185078204867346250733489663015417879915436157806942021693920206071715538430633494012923651469196048546309592946901609803631751035364478773126967010589504275776307
e1 = 3747
e2 = 2991
c1 = 24426579024062518665031958216110619832653602343205488454298659533869220501923184793828421371206493659949730138867555889074137026401207985428160803910695088081370233571905915349589146504374710444468715701305061060934519410886010929009297226496448218819742287990364436349188987723637449590579092391100714056589967894609950537021838172987840638735592599678186555961654312442380755963257875487240962193060914793587712733601168204859917001269928487633954556221987632934190217367502677285906521385169669644977192556145782303526375491484736352799180747403161343130663661867413380222714012960607473395828938694285120527085083
c2 = 6932145147126610816836065944280934160173362059462927112752295077225965836502881335565881607385328990881865436690904056577675885697508058289570333933837515526915707121125766720407153139160751343352211421901876051228566093038929625042619250168565502734932197817082848506826847112949495527533238122893297049985517280574646627011986403578166952789317461581409161873814203023736604394085875778774834314777046086921852377348590998381648241629124408514875110073073851913857329679268519229436092660959841766848676678740851087184214283196544821779336090434587905158006710112461778939184327386306992082433561460542130441825293
"""

【解析】

观察代码，给了两个e，下面来推一下攻击过程

已知：

$c1=m^{e1} \pmod n \\ c2 = m^{e2} \pmod n$

由贝祖定理

$a\cdot x_0+b\cdot y_0 = \gcd (a,b) \\ a\cdot x+b\cdot y = d$

若a，b是整数，且$\gcd(a, b)=d$，那么对于任意整数x，y，$a\cdot x+b\cdot y$都是d的倍数；且一定存在唯一的整数x，y，使$a\cdot x_0+b\cdot y_0=d$

带入c1和c2

$c1\cdot c2=m^{e1+e2} \pmod n$

用拓展欧几里得算法来求s1和s2，即

$e1\cdot s1+e2\cdot s2 = \gcd(e1, e2)$

下面推导一下拓展欧几里得算法是如何根据e1，e2来求得s1与s2的

拓展欧几里得算法

了解拓展欧几里得算法之前，先讲一下欧几里得算法

已知有整数a，b（不妨设a>b），$g=\gcd(a,b)$

有

$a = k_1\cdot b+r_1\\ r_1=a\%b$

（$k_1$为任意整数，$r_1$为a%b的余数）

两边同时除以整数g，得

$\frac{a}{g}=k_1\cdot\frac{b}{g}+\frac{r_1}{g}$

因为g是a，b的最大公因数（$g|a$ 且 $g|b$），即$\frac{a}{g}$，$\frac{b}{g}$都是整数

根据上式，整数之间的加减乘运算，那么$\frac{r_1}{g}$也是整数，即g 也是$r_1$的因子，而且$a = k_1\cdot b+r_1\to$ （$a>b>r_1$），g是a，b的最大公因数，那么g也是$r_1$的最大公因数。

欲求a，b的最大公因数，即求b与$r_1$的最大公因数。（$a>b>r_1$，数值减小）

继续，$b=k_2\cdot r_1+r_2$，同理g是$r_2$的最大公因数（$r_2=b\%r_1$）

此时，我们列出我们得到的这两个式子看看

$\begin{align*} a&=k_1\cdot b+r_1\\ b&=k_2\cdot r_1+r_2 \end{align*}$

那么等式右边第一项（原来b的位置）的数会越来越小，逐渐靠近0，到0就是这个递归的边界（$b`=0 $）。

最终

$\begin{align*} a&=k_1\cdot b+r_1\\ b&=k_2\cdot r_1+r_2\\ r_1&=k_3\cdot r_2+r_3\\ &……\\ r_{n-1}&=k_{n+1}\cdot r_n+0……①\\ r_{n}&=k_{n+2}\cdot 0+g \end{align*}$

递归：递归的本质是归约，把一个困难的问题转化为另一个简单的问题，且这个简单问题和前者是同一个问题，那么我们称为归约。

递归流水线：

$\begin{align*} \gcd(a,b)&=\gcd(b,r_{1})\\ &=\gcd(r_1,r_2)\\ &=\gcd(r_2,r_3)\\ &……\\ &=\gcd(r_{n-1},r_n)\\ &=\gcd(r_n,0)\\ \end{align*}$

而因为0除以任何数都为一个整数0，那么所有数都是0的因子（$\frac{0}{k}=0\to $$k|0$）。

则$\gcd(r_n,0)=r_n$，$r_n$与0的最大公因数就是$r_n$本身。

现在我们来看一下拓展欧几里得算法

续上

有$g=r_n$ ，$r_{n-1}>r_n$

$\begin{align*} r_{n-1}\cdot x_n~~~ +~~~ r_n\cdot y_n~~~~&=\gcd(r_{n-2},r_{n-1})\\ r_{n-2}\cdot x_{n-1} + r_{n-1}\cdot y_{n-1}&=\gcd(r_{n-3},r_{n-2})\\ \end{align*}$

且$r_{i+2}$%$r_{i+1}=r_i$

$\Bigg\lceil{r_{n-1}=r_{n-3}\%r_{n-2}}\\r_{n-2}=r_{n-4}\%r_{n-3}$

则有

$\begin{align*} g &=\gcd(r_{n-2},r_{n-1})\\ &= r_{n-1}\cdot x_n+r_n\cdot y_n \\ &=r_{n-1}\cdot x_n+(r_{n-2}\%r_{n-1})\cdot y_n \\ &=r_{n-1}\cdot x_n+[r_{n-2}-(r_{n-2}/r_{n-1})\cdot r_{n-1}]\cdot y_n \\ &=r_{n-1}\cdot x_n+r_{n-2}\cdot y_n-(r_{n-2}/r_{n-1})\cdot r_{n-1}\cdot y_n \\ &=r_{n-2}\cdot y_n+r_{n-1}\cdot [x_n-(r_{n-2}/r_{n-1})\cdot y_n ] \end{align*}$

且有

$g=\gcd(r_{n-3},r_{n-2})=r_{n-2}\cdot x_{n-1}+r_{n-1}\cdot y_{n-1}$

则

$\begin{align*} x_{n-1}&=y_n\\ y_{n-1}&=x_n-(r_{n-2}/r_{n-1})\cdot y_n \end{align*}$

代码实现为

def exgcd(a, b):
    if b == 0:
        return a, 1, 0
    g, x, y = exgcd(b, a%b)
    return g, y, x - (a//b)*y

搞定了拓展欧几里得算法，

求得s1与s2

$c1^{s1}\cdot c2^{s2}\equiv m^{e1\cdot s1+e2\cdot s2}\equiv m^{\gcd(e1,e2)} \pmod n$

如果e1与e2得最大公因数是1，那么我们就可以直接得到m

实践下来会发现$\gcd(e1,e2)$为3，那么因为剩下的指数很小，爆破一下k就可以出m（小明文攻击）

$m = (c1^{s1}\cdot c2^{s2}+k\cdot n)^{\frac{1}{3}}$

【EXP】

from Crypto.Util.number import *
import gmpy2


n = 27855350163093443890983002241607629119744539643165776358993469078731521668677421483556132628708836721737685936980427467856642738196111748018522018598646125626995613169001111504706363742194664774823604738939411512861441742683157275818500991834651769368178320088982759626122029956515159435424882855075032400667120376075618896752694718491438251810609878021717559466498493103257912108879328270813061231904227056671621363669388496383136964549879459562004569059185078204867346250733489663015417879915436157806942021693920206071715538430633494012923651469196048546309592946901609803631751035364478773126967010589504275776307
e1 = 3747
e2 = 2991
c1 = 24426579024062518665031958216110619832653602343205488454298659533869220501923184793828421371206493659949730138867555889074137026401207985428160803910695088081370233571905915349589146504374710444468715701305061060934519410886010929009297226496448218819742287990364436349188987723637449590579092391100714056589967894609950537021838172987840638735592599678186555961654312442380755963257875487240962193060914793587712733601168204859917001269928487633954556221987632934190217367502677285906521385169669644977192556145782303526375491484736352799180747403161343130663661867413380222714012960607473395828938694285120527085083
c2 = 6932145147126610816836065944280934160173362059462927112752295077225965836502881335565881607385328990881865436690904056577675885697508058289570333933837515526915707121125766720407153139160751343352211421901876051228566093038929625042619250168565502734932197817082848506826847112949495527533238122893297049985517280574646627011986403578166952789317461581409161873814203023736604394085875778774834314777046086921852377348590998381648241629124408514875110073073851913857329679268519229436092660959841766848676678740851087184214283196544821779336090434587905158006710112461778939184327386306992082433561460542130441825293



t = gmpy2.gcd(e1,e2)
print(t)
s,x,y = gmpy2.gcdext(e1,e2)
if t == 1:
    m = (pow(c1,x,n)*pow(c2,y,n)) % n
    print(long_to_bytes(m))
else:
    for k in range(1000):
        m = gmpy2.iroot((pow(c1,x,n)*pow(c2,y,n)%n + k*n),t)
        if m[1]:
            print(long_to_bytes(m[0]))
            break
        else:
             k += 1

【flag】

1	BaseCTF{feb7e1ae-a8f7-4fc4-8d6d-945a45cc3f6d}

========================================================================================

ez_log

【想法】：爆破，2**7-1的范围也不是很大

【题目】

from Crypto.Util.number import bytes_to_long as b2l, long_to_bytes as l2b, getPrime
from Crypto.Cipher import AES
from random import randint


flag = b"flag{test_flag}"

pad = lambda x: x+b'\x00'*(16-len(x)%16)

def encrypt(KEY):
    cipher= AES.new(KEY,AES.MODE_ECB)
    encrypted =cipher.encrypt(flag)
    return encrypted

def decrypt(KEY):
    cipher= AES.new(KEY,AES.MODE_ECB)
    decrypted =cipher.decrypt(enc)
    return decrypted

flag = pad(flag)
x = randint(10 ** 7, 10 ** 8)
y = randint(10 ** 7, 10 ** 8)
n = getPrime(28)
z = pow(y, x, n)

enc = encrypt(pad(l2b(x)))
print(f'enc = {b2l(enc)}')
print(f'y = {y}')
print(f'n = {n}')
print(f'z = {z}')

'''
enc = 33416570913716503492297352041317858420349510954381249751537743898024527101872454706181188441210166165803904185550746
y = 82941012
n = 228338567
z = 51306718
'''

【解析】

解法一：

爆破x，然后AES解密

解法二（预期解）：

离散对数求解

【EXP】

from Crypto.Util.number import bytes_to_long , long_to_bytes , inverse
from Crypto.Cipher import AES

x = 10**7
enc = 33416570913716503492297352041317858420349510954381249751537743898024527101872454706181188441210166165803904185550746
y = 82941012
n = 228338567
z = 51306718


'''while(pow(y, x, n)!=z and x<10**8):
    x+=1
    if(x%1000000==0):
        print(x)
print("x=",x)
'''
x = 38806815
pad = lambda x: x+b'\x00'*(16-len(x)%16)
def decrypt(KEY):
    cipher= AES.new(KEY,AES.MODE_ECB)
    decrypted =cipher.decrypt(long_to_bytes(enc))
    return decrypted

m = decrypt(pad(long_to_bytes(x)))

# 去除填充
flag = m.rstrip(b'\x00').decode()

print(flag)

离散对数求解

# sagemath
from Crypto.Cipher import AES
from Crypto.Util.number import bytes_to_long , long_to_bytes 

pad = lambda x: x+b'\x00'*(16-len(x)%16)

def decrypt(KEY):
    cipher= AES.new(KEY,AES.MODE_ECB)
    decrypted =cipher.decrypt(enc)
    return decrypted

enc = 33416570913716503492297352041317858420349510954381249751537743898024527101872454706181188441210166165803904185550746
y = 82941012
n = 228338567
z = 51306718

enc = long_to_bytes(enc)
G = GF(n)
z = G(z)
y = G(y)
x = discrete_log(z, y)


print(decrypt(pad(long_to_bytes(x))))

# BaseCTF{BF3DCONZ-67FE-ENZU-385S-CSNI13B2}

【flag】

1	BaseCTF{BF3DCONZ-67FE-ENZU-385S-CSNI13B2}

========================================================================================

wiener

【想法】：第一次见到这种给小数的wiener

【题目】

from Crypto.Util.number import *
import decimal
flag=b"BaseCTF{}"
m = bytes_to_long(flag)


p = getPrime(1024)
q = getPrime(1024)
n=p*q

e=65537
c=pow(m,e,n)

print("e =",e)
print("c =",c)

decimal.getcontext().prec = 648
P=decimal.Decimal(p)
Q=decimal.Decimal(q)
leak=decimal.Decimal((3*P*Q-1)/(3*Q*Q))
print("leak =",leak)

"""
e = 65537
c = 11032748573623426359632659657114807044712138586316710250985606809252700461490504487308849626514319062562557448839550994242999334882617031487618174168038491566640081840111747765753878087564318833273878755416584962921669911444225959335274753391800995531023212276838665202257007640354237043291129197348884914956663597240094662207929658519596987351984403258345205873566463643624175318315064440456858013874962784792564480286904620663695194689839431808082976248378509181327101557380978849545906691903896662095520288964101796965095129861467059775556110616007889846240936219381379219605528051627402300580239311202137582442057
leak = 0.829374344780877053838760251345359097311540811993463349625630085472892814959843248358036249898871908548743719153319438638517170060651237635838827482534816419091949205584951292517303330452910012749674475329235689229498752425379611083979518257734473992186831474208400813283887045691145481237726578827559198828469462343342343287720369159899636816373592067698883361360269728719786071024354151682314608072902347335691012713629816579496252896260869382806838857194293618332286500427694077400072428506897829689703872985954772105672992293334668485358785863779749153981721900135318166811250762946069962348114491411585418993494561587403918162681937152503739843
"""

【解析】

wiener解决连分数

$\begin{align*} leak &= \frac{3\cdot P\cdot Q-1}{3\cdot Q\cdot Q}\\ &= \frac{P}{Q}-\frac{1}{3\cdot Q\cdot Q} \end{align*}$

连分数定理

其中也用到了辗转相除法的思想

定义

当a和b满足

$|x-\frac{a}{b}|<\frac{1}{2\cdot b^2}$

时，则$\frac{a}{b}$是x的一个连分数近似。

例子

把 $\frac{1314}{520}$ 进行连分数展开，形式就是对分子分母做辗转相除。

$\begin{align*} \frac{1314}{520} &= 2+\frac{274}{520}\\\\ \frac{520}{274} ~&= 1+\frac{246}{274}\\\\ \frac{274}{246} ~&=1+\frac{32}{246}\\\\ \frac{246}{32} ~&=7+\frac{22}{32}\\\\ \frac{32}{22} ~&=1+\frac{10}{22}\\\\ \frac{22}{10} ~&=2+\frac{2}{10}\\\\ \frac{10}{2} ~&=5+0 \end{align*}$

所以 $\frac{1314}{520}$ 展开连分数为

$\frac{1314}{520}=2+\frac{1}{1+\frac{1}{1+\frac{1}{7+\frac{1}{1+\frac{1}{2+\frac{1}{5+0}}}}}}$

运用

可以从上面一个例子看出，

我们通过连分数展开可以轻松知道每一层的分子与分母，如果对无理数或者两个很大的数字分数进行连分数展开，那么我们会得到很多很多层分子分母，此时就可以只拿较多的层数，然后计算成一个分数，得到其的一个近似值

还是 $\frac{1314}{520}$ ，我们从连分数展开的第四层断开，即把7后面的分式约等于0

有

$\begin{align*} \frac{1314}{520}&\approx2+\frac{1}{1+\frac{1}{1+\frac{1}{7+0}}}\\ &=2+\frac{1}{1+\frac{1}{\frac{8}{7}}}\\ &=2+\frac{1}{\frac{15}{8}}\\ &=\frac{38}{15} \end{align*}$

即 $\frac{1314}{520}$ 的近似值为 $\frac{38}{15}$

这么，我们可以从一个小数中拿到其近似值的分子与分母，也可以从一个分数中提取分子与分母

【EXP】

# sagemath
from Crypto.Util.number import *

e = 65537
c = 11032748573623426359632659657114807044712138586316710250985606809252700461490504487308849626514319062562557448839550994242999334882617031487618174168038491566640081840111747765753878087564318833273878755416584962921669911444225959335274753391800995531023212276838665202257007640354237043291129197348884914956663597240094662207929658519596987351984403258345205873566463643624175318315064440456858013874962784792564480286904620663695194689839431808082976248378509181327101557380978849545906691903896662095520288964101796965095129861467059775556110616007889846240936219381379219605528051627402300580239311202137582442057
leak = 0.829374344780877053838760251345359097311540811993463349625630085472892814959843248358036249898871908548743719153319438638517170060651237635838827482534816419091949205584951292517303330452910012749674475329235689229498752425379611083979518257734473992186831474208400813283887045691145481237726578827559198828469462343342343287720369159899636816373592067698883361360269728719786071024354151682314608072902347335691012713629816579496252896260869382806838857194293618332286500427694077400072428506897829689703872985954772105672992293334668485358785863779749153981721900135318166811250762946069962348114491411585418993494561587403918162681937152503739843

cf = continued_fraction(leak)
cfs = cf.convergents()
print(cf)
for i in cfs:
    p, q = i.as_integer_ratio()
    p, q = int(p), int(q)
    if p.bit_length() == 1024 :
        phi = (p-1)*(q-1)
        d = int(inverse(e, phi))
        m = int(pow(c, d, p*q))
        flag = long_to_bytes(m).decode()
        print(flag)

【flag】

1	BaseCTF{9431ee53-5d5c-4b0b-956f-1eafff6c9e87}

========================================================================================

没有n啊

【想法】：给了有关n的leak，那么先解出n，再解c

【题目】

from Crypto.Util.number import *
import gmpy2

flag=b'BaseCTF{}'
m=bytes_to_long(flag)

p=getPrime(512)
q=getPrime(512)

n=p*q
e=65537

phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)

c=pow(m,e,n)
x=pow(n,e,c)
print("c =",c)
print("e =",e)
print("d =",d)
print("x =",x)
'''
c = 52453423663797600504896811946820841317615798875871627840172711423749946998217916744135290476795328543876098295227017753117609268701786914053599060330837226980969490439739651088710549890669593587642238827462108900683237797139569260570711611781514337884756698142193277516649805710242748531658979160170193283558
e = 65537
d = 54297831548863701092644190086258072883163378307246681513317422545902442650340916001357605211715836911877651782099787873046987096258918495734824011752504203578982947618784736181975847356304742402103468329660346526185908618978851982007496096394151821403282347897417590596861323293706611997134962231129075032641
x = 40635864473997460751766935373772107585133301579524000836637683731949939348171187931595274511243052505604832873086269554842194695737052043633079044688826020656068356561856848814530947955429343483847291398607359454851926470168457852479044154798114087493843073091985855839008222762224952503563764527380033064437
'''

【解析】

虽然给了d，但这是解密m的密钥d1，并不是解密n的密钥d2，所以我们还得单独计算d2

先去 factordb.com 分解c，从而计算c的phi，根据

Snipaste55

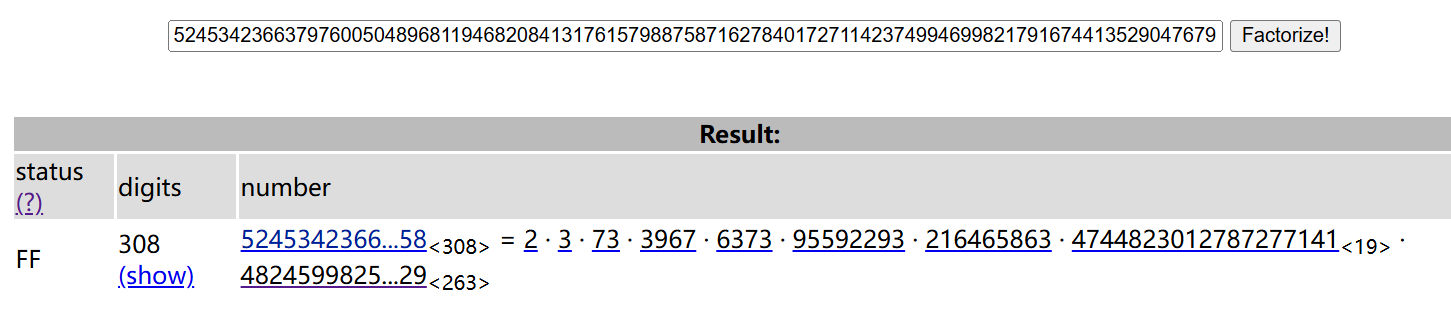
Snipaste23

知道c是合数，那么其欧拉函数是每个因子减一后相乘。

得到d2，后RSA解密得到n-c

因为n>c，在给nRSA加密时，mod c抹去了n部分信息，那么我们在解密时也要加k倍的c来还原n

再正常的解RSA就好了。

【EXP】

from Crypto.Util.number import long_to_bytes
from gmpy2 import invert
11015260047934780052747294376733821095287179138785591145017290559502196403082643165843965160935284779466935313070299057142775556894470097468695819752254792507921123107002935788077406049952740095685723668194899869965191737455279007950292408390923302696060771579231969440445447866191691818829900264135305035739551749    
c = 52453423663797600504896811946820841317615798875871627840172711423749946998217916744135290476795328543876098295227017753117609268701786914053599060330837226980969490439739651088710549890669593587642238827462108900683237797139569260570711611781514337884756698142193277516649805710242748531658979160170193283558
e = 65537
d = 54297831548863701092644190086258072883163378307246681513317422545902442650340916001357605211715836911877651782099787873046987096258918495734824011752504203578982947618784736181975847356304742402103468329660346526185908618978851982007496096394151821403282347897417590596861323293706611997134962231129075032641
x = 40635864473997460751766935373772107585133301579524000836637683731949939348171187931595274511243052505604832873086269554842194695737052043633079044688826020656068356561856848814530947955429343483847291398607359454851926470168457852479044154798114087493843073091985855839008222762224952503563764527380033064437

c_list = [2 , 3 , 73 , 3967 , 6373 , 95592293 , 216465863 , 4744823012787277141 ,48245998253859255581546561942142167304434549996919484957120717763726325509833409296170471619434291990255044694414983821250538266717293535917534918221352198192885071310932646412147737114561229291373456448363184353049796801297876664512630305475226391199481032049429]
c_phi = 1
for i in range(len(c_list)):
    c_phi *= c_list[i] - 1
d_c = invert(e, c_phi)
n = int(pow(x, d_c, c)+c)
print(n)
print("n=",n)
print(x==pow(n,e,c))

m = pow(c, d, n)
print(m==608975871998468334256789566495307620134871095774360271136884525677002770227977521307197556863857539091282045)
flag = long_to_bytes(int(m))
print(flag)

【flag】

1	BaseCTF{2eefa8ef-ba57-4bed-9230-d280ac2273d8}

========================================================================================

没有n啊_pro

【想法】：这次没有给n的leak，那么就看看能不能通过ed方程解

【题目】

from Crypto.Util.number import *
import gmpy2

flag=b'BaseCTF{}'
m=bytes_to_long(flag)
p=getPrime(128)
q=getPrime(128)

n=p*q
e=65537

phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)

assert d<phi

c=pow(m,e,n)
print("c =",c)
print("e =",e)
print("d =",d)
"""
c = 78919950899709764543039048006935881842075789773495004639436106636461009323420
e = 65537
d = 13002488326322253055272696035053386340217207134816593767440035447757509399233
"""

【解析】

给了c，d，e

有

$e\cdot d \equiv 1 \mod{\phi (n)}\\ e\cdot d-1=k\cdot \phi (n)……①\\ 且\\ d<\phi(n)……②$

解法一：

对①改造一下

$e\cdot d\approx k\cdot \phi(n)$

又有②$d<\phi(n)$，那么$e>k$

从而知道了k的范围 0~e ，相当于我们已经知道了k

四个参数中，有两个已知数，一个可以爆破，那么我们可以求另一个的可能集合[phi1, phi2…… phi n]

再用这个集合去分解得到p和q，然后正常解RSA

【EXP】

# sagemath  time_speed 31.9s
from Crypto.Util.number import *
import itertools
c = 78919950899709764543039048006935881842075789773495004639436106636461009323420
e = 65537
d = 13002488326322253055272696035053386340217207134816593767440035447757509399233
p_bits=128
q_bits=128
def get_phi(e, d):
    k_phi = e*d -1
    result = []
    for k in range(e,2,-1):
        if k_phi % k == 0:
            tmp = k_phi // k
            if int(tmp).bit_length()==p_bits+q_bits:
                result.append(tmp)
    return result
def main():
    phi_list = get_phi(e,d)  #获得可能的phi_n列表
    count = len(phi_list)
    print(f'一共有{count}个可能的phi')
    count = 0
    for phi in phi_list:
        count += 1
        print(f'{count} 正在尝试爆破 {phi}')
        factors = factor(phi)  # 分解phi_n得到质因子列表
        result = []
        for i in factors:
            num, times = int(i[0]), i[1]
            result += [num] * times

        if len(factors)>1:
            s = set()
            for r in range(1, len(result) + 1):
                combination = list(itertools.combinations(result, r))
                for i in combination:
                    s.add(i)
            ans=[]
            for i in s:
                tmp=1
                for j in i:
                    tmp=tmp*j
                ans.append(tmp)
            for num in ans:
                if int(num+1).bit_length()==p_bits and is_prime(num+1):
                    p = num+1
                    q = phi // num + 1
                    if is_prime(q):
                        n = p * q
                        flag=long_to_bytes(int(pow(c,d,n)))
                        if b'BaseCTF' in flag:
                            print(flag)
                            return


if __name__ == '__main__':
    main()

【flag】

1	BaseCTF{3e226a94-babb27696416}

========================================================================================

week4

extendmd5

【想法】：不输入然后直接返回给的md5

【题目】

from Crypto.Util.number import *
import hashlib
import socketserver
import os
import random 
flag = os.getenv('GZCTF_FLAG')


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self):
        return self._recvall()

    def my_md5(self,text):
        mymd5=hashlib.md5()
        mymd5.update(text)
        return mymd5.hexdigest()
    def handle(self):
        for _ in range(100):
            c=random.randint(32,63)
            want=random.randbytes(c)
            want_md5=self.my_md5(want)
            self.send(want_md5.encode())

            while True:
                self.send(b"\nPlease input the secret:")
                secret = self.recv()

                final=want+secret
                final_md5=self.my_md5(final)

                self.send(b"\nPlease input your md5:")
                your_md5=self.recv().decode()
                if final_md5 == your_md5:
                    self.send(b'correct!')
                    break
                else :
                    self.send(b'wrong!')
    
        self.send(flag.encode())
        self.send(b"\nConnection has been closed  =.=  ")
        self.request.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 9999
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

【解析】

md5扩展攻击

参考浅谈HASH长度拓展攻击 - Yunen的博客 - 博客园 (cnblogs.com)

题目给了一串由want生成的md5值A1，然后允许我们输入一串字符，添加在want变量后面，然后服务器再计算MD5值A2，我们要自己输入这个MD5值A3，然后服务器比较验证两个MD5（A2==A3）是否相同。

def handle(self):
    for _ in range(100):
        c=random.randint(32,63)
        want=random.randbytes(c)
        want_md5=self.my_md5(want)
        self.send(want_md5.encode())

        while True:
            self.send(b"\nPlease input the secret:")
            secret = self.recv()

            final=want+secret
            final_md5=self.my_md5(final)

            self.send(b"\nPlease input your md5:")
            your_md5=self.recv().decode()
            if final_md5 == your_md5:
                self.send(b'correct!')
                break
            else :
                self.send(b'wrong!')

MD5

参考【CRYPTO】哈希长度拓展攻击 | 狼组安全团队公开知识库 (wgpsec.org)

填充方法（补足长度成一个分组，方便hash）

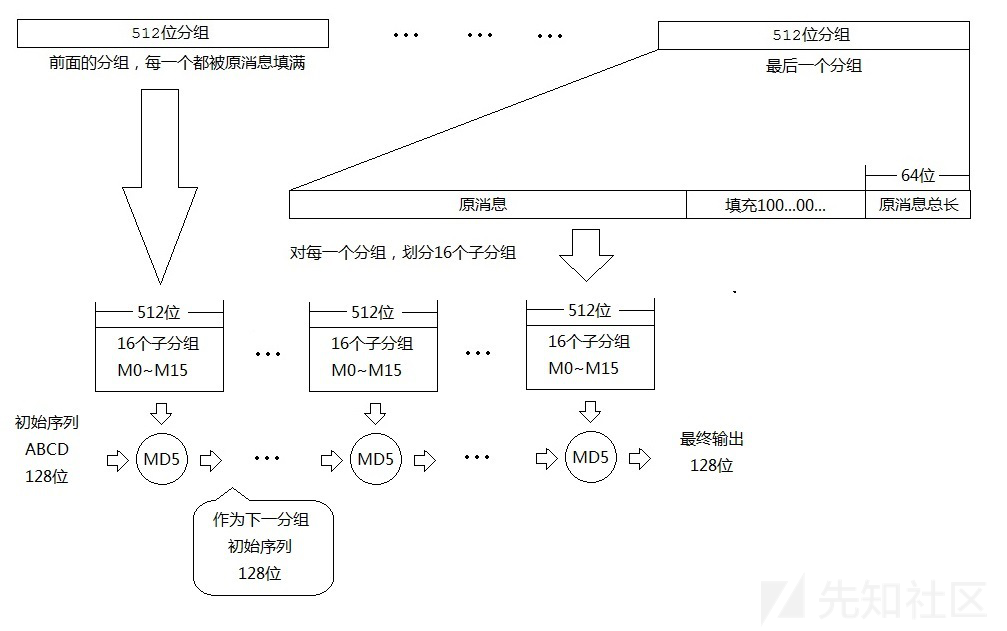
图片摘自：哈希长度拓展攻击(Hash Length Extension Attacks)

当hash函数拿到需要被hash的字符串后，先将其字节长度对64取模。如果余数正好等于56，那么就在该字符串最后添加上8个字节的长度描述符（具体用bit表示）。如果不等于56，就先对字符串进行长度填充，填充时规定第一个字节为hex(80)，其余字节均用hex(00)填充，填充至余数为56以后，增加8个字节的长度描述符（该长度描述符为需要被hash的字符串的长度，不是填充之后整个字符串的长度）。

若余数超过56，那么还得再用填充字符\x80\x00……来填充成新的一块，到下一块的第56位停止到加上明文长度的十六进制表达

长度描述符的填入方式

注意MD5运算的时候是小端序存储，假设我们最后8个字节的值为0000001234567890那么存储在MD5运算时的存储方式为9078563412000000，每两个字节构成一个十六进制并且按照逆序的顺序存储。

例如

计算aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaabbb60个a和3个b

转一下hex

填充

那么填充后是下图，填充了57（即64*2-63-8）个填充符（一个\x80和56个\x00）

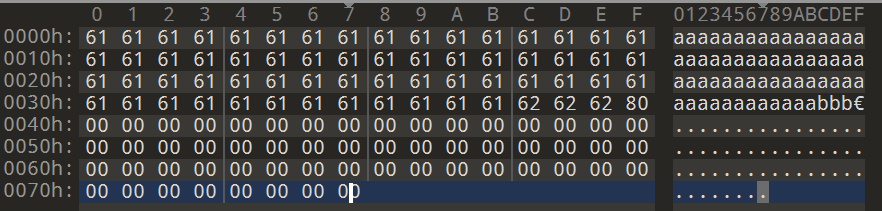
加上长度描述符（8位十六进制）

63的十六进制是\x3f，采用小端序存储

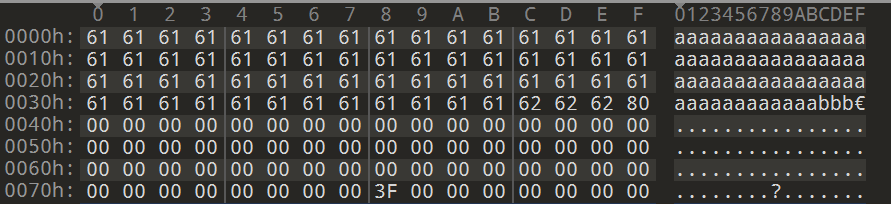
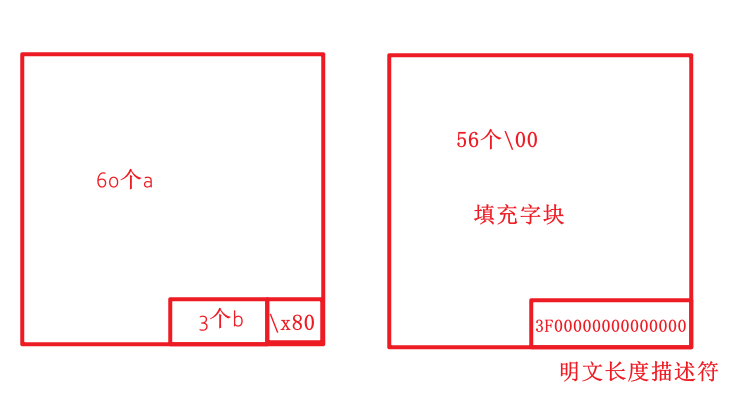
计算过程

参考浅谈HASH长度拓展攻击 - Yunen的博客 - 博客园 (cnblogs.com)

一开始有个初始VI

A=0x67452301
B=0xefcdab89
C=0x98badcfe
D=0x10325476

这串初始向量的值是固定的，作为与第一块数据运算的原始向量。

当这串向量与第一块数据块运算之后，得到了一串新的向量值，这串新的向量值接着与第二块数据块参加运算，直到最后一块数据块。

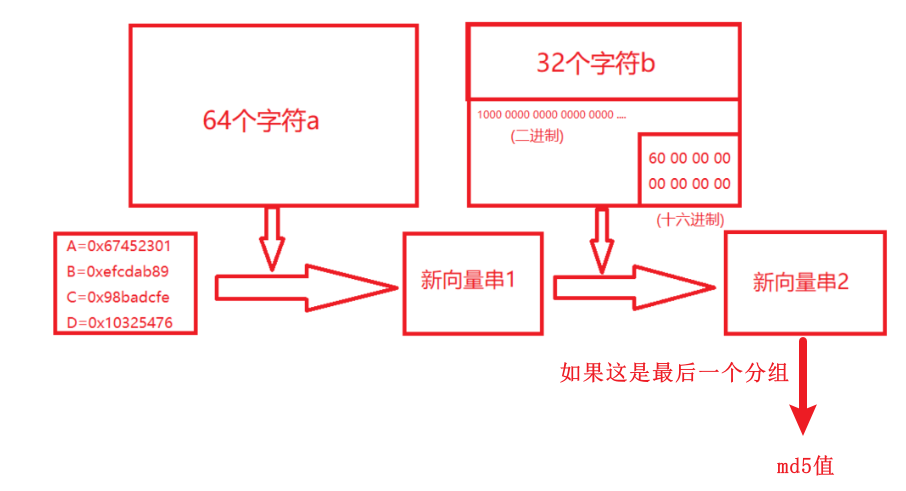
VI与md5值相转换的过程

“ “ “而最后的MD5值就是这最后的向量串经过如下转换的结果。

如向量串：

A=0xab45bc01
B=0x6a64bb53
C=0x23ba8afe
D=0x46847a62

先两两为一组进行组合，得到如下数据：

ab 45 bc 01
6a 64 bb 53
23 ba 8a fe
46 84 7a 62

再进行高低位互换，得到如下数据：

01 bc 45 ab
53 bb 64 6a
fe 8a ba 23
62 7a 84 46

最终拼接得到MD5值：01bc45ab53bb646afe8aba23627a8446。 ” ” ”

那么MD5值也可以逆推到VI。

攻击方法

已知前几块的md5，那么我们可以利用这个md5构造一个新的初始VI，然后与我们构造的“填充字块”+B去计算md5

当然还要跳过省略前面的分组

例子

还是上面那个，我们现在只知道有63个字符，那么已经超过了一个块，那么我们自己帮它填充并加上长度描述符，再在后面添加任意字符，使得这个任意字符单独在一个新的分组中，不干扰前面的MD5计算。

但这里还是有个问题（我也不太清楚）：md5函数能自己识别我填充的字符和长度描述符吗？它会不会把我自己加的这些也当成了前面的明文来计算一个新的md5吗。

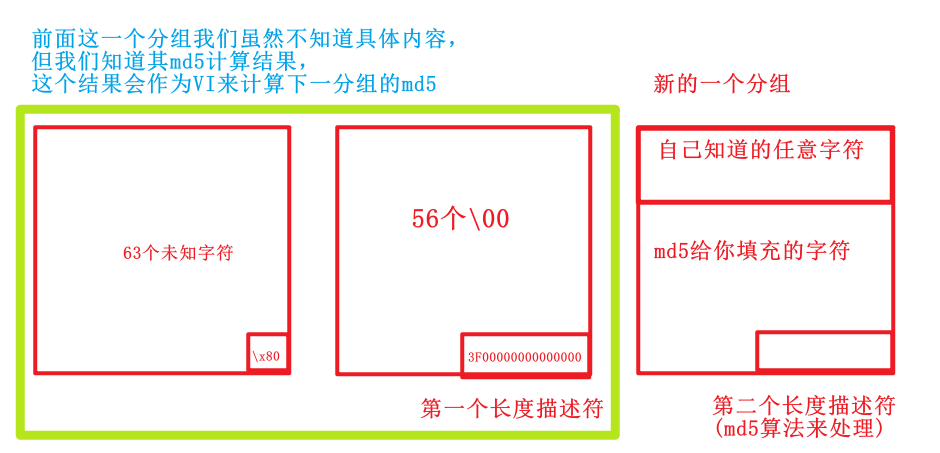
这就是md5拓展攻击

流程图

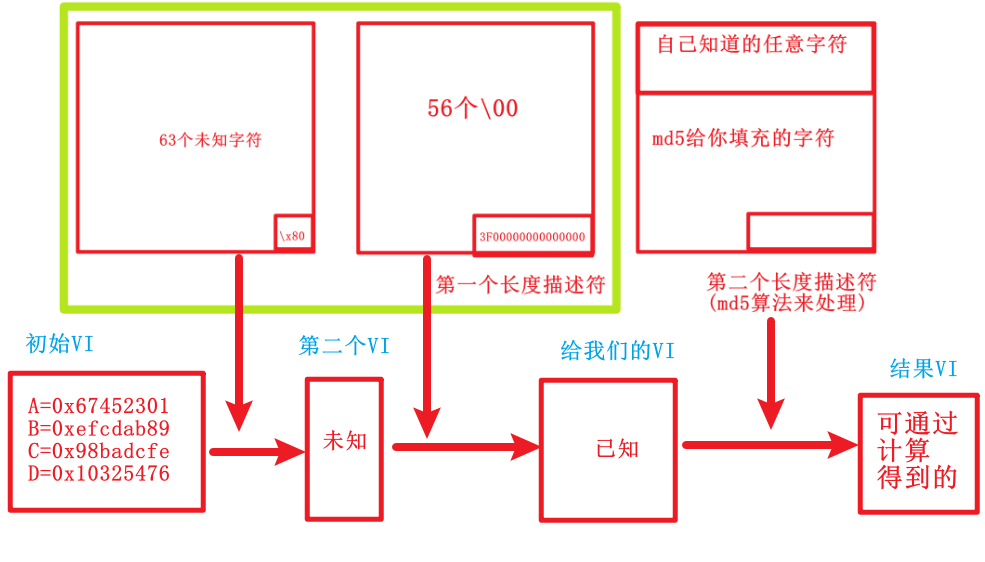
这题还需要爆破明文长度

【EXP】

脚本来源：naby

from pwn import *

import struct
import math

# 定义MD5所需的常量
T = [int(4294967296 * abs(math.sin(i + 1))) & 0xFFFFFFFF for i in range(64)]


# 定义左旋转函数
def left_rotate(x, c):
    return (x << c) | (x >> (32 - c))


# 定义MD5主循环所需的四个基本函数
def F(x, y, z):
    return (x & y) | (~x & z)


def G(x, y, z):
    return (x & z) | (y & ~z)


def H(x, y, z):
    return x ^ y ^ z


def I(x, y, z):
    return y ^ (x | ~z)


# 定义MD5算法
def my_md5(message, A, B, C, D, skip):
    # 初始化变量
    a, b, c, d = A, B, C, D

    # 填充消息
    original_length = len(message) * 8
    message += b'\x80'
    while (len(message) * 8) % 512 != 448:
        message += b'\x00'
    message += struct.pack('<Q', original_length)

    # 处理每个512位（64字节）块
    # 跳过前几个分组
    for i in range(64 * skip, len(message), 64):
        block = message[i:i + 64]
        X = struct.unpack('<16I', block)

        # 备份当前的a, b, c, d值
        AA, BB, CC, DD = a, b, c, d
        # 进行四轮操作，每轮16步
        for i in range(64):
            if 0 <= i <= 15:
                k, s, func = i, [7, 12, 17, 22][i % 4], F(b, c, d)
            elif 16 <= i <= 31:
                k, s, func = (5 * i + 1) % 16, [5, 9, 14, 20][i % 4], G(b, c, d)
            elif 32 <= i <= 47:
                k, s, func = (3 * i + 5) % 16, [4, 11, 16, 23][i % 4], H(b, c, d)
            elif 48 <= i <= 63:
                k, s, func = (7 * i) % 16, [6, 10, 15, 21][i % 4], I(b, c, d)

            temp = b + left_rotate((a + func + X[k] + T[i]) & 0xFFFFFFFF, s)
            a, b, c, d = d, temp & 0xFFFFFFFF, b, c

        # 将结果加到当前的a, b, c, d
        a = (a + AA) & 0xFFFFFFFF
        b = (b + BB) & 0xFFFFFFFF
        c = (c + CC) & 0xFFFFFFFF
        d = (d + DD) & 0xFFFFFFFF
    # 返回哈希结果
    return struct.pack('<4I', a, b, c, d).hex()


rem = remote("", )

for _ in range(100):
    want_md5 = rem.recv(32).decode()  # 接收原始数据的md5

    # 计算成iv
    iv = []
    for i in range(4):
        tmp = ""
        for j in range(4):
            tmp += want_md5[(i + 1) * 8 - (j + 1) * 2:(i + 1) * 8 - j * 2]
        iv.append(int(tmp, 16))

    # 爆破长度
    for i in range(32, 64):
        rem.recvuntil(b"Please input the secret:")

        # 填充消息
        payload = b''
        payload_length = i * 8
        payload += b'\x80'
        while ((i + len(payload)) * 8) % 512 != 448:
            payload += b'\x00'
        payload += struct.pack('<Q', payload_length)
        payload += b'naby'

        rem.sendline(payload)

        # 计算填充数据后的有几个分组，需要跳过计算
        skip = (i + len(payload) - 4) // 64
        A, B, C, D = iv
        message = b'a' * (64 * skip) + b'naby'
        res = my_md5(message, A, B, C, D, skip)
        rem.recvuntil(b"Please input your md5:")
        rem.sendline(res.encode())
        rem.recvline()
        m = rem.recvline()
        if b'correct' in m:
            print(_, want_md5, i, m)
            break

rem.interactive()

脚本解析

# 定义MD5所需的常量
T = [int(4294967296 * abs(math.sin(i + 1))) & 0xFFFFFFFF for i in range(64)]


# 定义左旋转函数
def left_rotate(x, c):
    return (x << c) | (x >> (32 - c))


# 定义MD5主循环所需的四个基本函数
def F(x, y, z):
    return (x & y) | (~x & z)


def G(x, y, z):
    return (x & z) | (y & ~z)


def H(x, y, z):
    return x ^ y ^ z


def I(x, y, z):
    return y ^ (x | ~z)


# 定义MD5算法
def my_md5(message, A, B, C, D, skip):
    # 初始化变量
    a, b, c, d = A, B, C, D

    # 填充消息
    original_length = len(message) * 8
    message += b'\x80'
    while (len(message) * 8) % 512 != 448:
        message += b'\x00'
    message += struct.pack('<Q', original_length)

    # 处理每个512位（64字节）块
    # 跳过前几个分组
    for i in range(64 * skip, len(message), 64):
        block = message[i:i + 64]
        X = struct.unpack('<16I', block)

        # 备份当前的a, b, c, d值
        AA, BB, CC, DD = a, b, c, d
        # 进行四轮操作，每轮16步
        for i in range(64):
            if 0 <= i <= 15:
                k, s, func = i, [7, 12, 17, 22][i % 4], F(b, c, d)
            elif 16 <= i <= 31:
                k, s, func = (5 * i + 1) % 16, [5, 9, 14, 20][i % 4], G(b, c, d)
            elif 32 <= i <= 47:
                k, s, func = (3 * i + 5) % 16, [4, 11, 16, 23][i % 4], H(b, c, d)
            elif 48 <= i <= 63:
                k, s, func = (7 * i) % 16, [6, 10, 15, 21][i % 4], I(b, c, d)

            temp = b + left_rotate((a + func + X[k] + T[i]) & 0xFFFFFFFF, s)
            a, b, c, d = d, temp & 0xFFFFFFFF, b, c

        # 将结果加到当前的a, b, c, d
        a = (a + AA) & 0xFFFFFFFF
        b = (b + BB) & 0xFFFFFFFF
        c = (c + CC) & 0xFFFFFFFF
        d = (d + DD) & 0xFFFFFFFF
    # 返回哈希结果
    return struct.pack('<4I', a, b, c, d).hex()

8到74行都是md5实现加上一点点魔改（skip变量来实现跳到最后一个块前）

我们只能添加尾巴，并不知道前面到底有多少字符，当然也不知道有多少块，进行过多少次md5计算才得到最后给我们的这串md5值。那自然就忽略了前面的块。

1	rem = remote("gz.imxbt.cn", 端口号)

77行远程连接

want_md5 = rem.recv(32).decode()  # 接收原始数据的md5

    # 计算成iv
    iv = []
    for i in range(4):
        tmp = ""
        for j in range(4):
            tmp += want_md5[(i + 1) * 8 - (j + 1) * 2:(i + 1) * 8 - j * 2]
        iv.append(int(tmp, 16))

80行到88行

接收md5值并转成VI

# 爆破长度
    for i in range(32, 64):
        rem.recvuntil(b"Please input the secret:")

        # 填充消息
        payload = b''
        payload_length = i * 8
        payload += b'\x80'
        while ((i + len(payload)) * 8) % 512 != 448:
            payload += b'\x00'
        payload += struct.pack('<Q', payload_length)
        payload += b'naby'

90行到101行

爆破最后一个分组的明文长度（模64的情况下）

# 计算填充数据后的有几个分组，需要跳过计算
        skip = (i + len(payload) - 4) // 64  # 后人记 这个应该是需要跳过的块
        A, B, C, D = iv
        message = b'a' * (64 * skip) + b'naby'
        res = my_md5(message, A, B, C, D, skip)
        rem.recvuntil(b"Please input your md5:")
        rem.sendline(res.encode())

用给的VI来计算我们的 任意字符（这里是出题人师傅的名字） 的md5值

【flag】

动态flag

可以去BaseCTF2024新生赛 - Review::CTF (imxbt.cn) 复现

题外话

这题我的想法可以执行，给个空输入，然后再输入回它给的md5值，结果也是返回“correct！”，属于非预期了

========================================================================================

hard_math

【想法】：还是矩阵，$|W|=|V|=|hint|\cdot |k|$ k是$\begin{bmatrix}0&b&c\\0&0&f\\0&0&0\end{bmatrix}$

然后格基归约，因为矩阵第一行位数与其他位相差甚大

【题目】

import numpy as np
from sage.all import *
from Crypto.Util.number import *

a, b, c = [getPrime(128) for _ in range(3)]
d, e, f, h, i, j = [getPrime(512) for _ in range(6)]
k, l, m = [getPrime(16) for _ in range(3)]

flag = b"flag{test_flag}"
n = len(flag) // 3
flag1 = bytes_to_long(flag[0:n])
flag2 = bytes_to_long(flag[n:2 * n])
flag3 = bytes_to_long(flag[2 * n:3 * n])
mat_flag = matrix([flag1, flag2, flag3])

def randomArray():
    upper = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
    low = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
    for i in range(3):
        for j in range(i+1, 3):
            upper[i][j] = getPrime(512)
            low[j][i] = getPrime(512)
    result = np.array(upper) @ np.array(low)
    return result

def m2l(data):
    data = str(list(data)).replace(')',']').replace('(','[')
    return data

U = matrix(randomArray())

V = matrix(
    [
        [a, b, c],
        [d, e, f],
        [h, i, j]
        ]
    )

hint = matrix(
    [
        [a, 0, 0],
        [d, e, 0],
        [h, i, j]
        ]
    )

W = U * V
r = matrix([k, l, m])

m = mat_flag * W + r

print(f'm = {m2l(m)}')
print(f'W = {m2l(W)}')
print(f'hint = {m2l(hint)}')

'''
m = [[515006066572991495094024845507453270170679530115722665716310857090383589987192995300820709326539907598036228187098433712764150545713781753928519780987397892019149396848734270629944247423448792576409939690690172467014798009304748201014701433638914639516136791514943818115581841161140822534657373450411916010383872732592192428514885246957165021151091735415512934159556555795946329029885077848428522565951230170422871166025743271004222458910631903580841388720000991656351499297814283656311006619217557, 493376106730590001882623910015696056521634040769204676097683956342407441946394989269289586462834183861958955979569597323143336033364245602994690452975858606246399021815786952339420761036368842534214572793543597526440971054273983326810410557306121368806745656400301215422355097611632518232563203326662080440857128552584680151063471311246027207795633032412326671372295196912352244705460776745840724990330443310670290805805114851081572848158034185286087423873359219385001802862944316920564177120955175, 575595002745228725017587011229401876567667455244528775277629732860064977911268125609189310020405051622085511289521885274600136190154096572813688714712133062373574937656504877555714680953922288909295838812970976406997779107157755042843766890628178252727891534572782306820699889220503146129501975505498358015202877369653016071954056645819683541482989501884449536172692222955049657627314349743452274317472117170325014443435968767431351069364374662221187031602748415650312412433222057689003403908801913]]
W = [[838243669569772365825528069088793455362253801517360278602593303745699429137215594576991203071727187689167097915523807181069815074124001330605476179062587774586413099179825273026676486841213151585743972214797692786366689785491273081413668402037800457578015835799910062278548422607854946333715446327802896293029377534443735084744391631685250614642775247173445704258033114931031666306649949263186126055241139290905429794696028384343749984236719592960909032270495356, 803037915525763017813052134194087092503024850450778985110871642829830991012170830783900056324370267494800927024749373592744933154087905523794957583458320772762393022274754812539413304654338911861881703406551975827547157103926858618050322166669434180444100312398454530810141984367238536123028456943329443614154050974619461000072847460724967548375623320227093428700111757757638270165456251865510363753235078534130529338200958418407734698270157192357964274092960160, 936860550979161859763944379815022616668684890898857549853283234781148589264637570580765176526871677402372007461081732898697312885010695317454774616907341062321919789905918536590631377401204453037238548216648108039082749895680446221612769807718147337667121814420180597640654236164929573894976873797106386019676593508260795149809742272019006821924426056135904099903987553221898726778429309630193632524365812002539064510798904913798165805952369467097166655052324662], [903827515929770485045352583923655902326985198425839313304983595578754651977406515523417091164606505992344067878304810153443237319663912774096105876828088267351880185653549590057499840375845602572585406606843113691398586082599896034026753671311127281701066533882077608584967968707777937945824307588234847645532828872891999612833211248100809726023940327229679170954992117211762654040526677026676750258569210085085849650693677075476712776614907076983085506292744593, 865867277899743984439472212248353523489475207105436612467388414274420933395815480684569358513658899128263451705767460689322324871155098437383762120083505456143481204507833625398191810324011750457183760477995450683492183216742470659735972303328300805612595535471688829946545404613937343154546265892485079288647073301566428063885748080397335579940733133160982445771626323095205883638294011960474082043462070600709609945253876118567904739848764175027352015971149441, 1010160142335093061390073894563508864471566280278502420921989223687002198547569470869775259447268733595903657260678484653049020541253485677709836243404433947659892982318145912957083642845032140875108225542486758247838327077646951588304929682753162881261192381472575935615608383217184248495268384377517552833159650113564246358248703626825695080546545844771964065265076038887828360524279438416928547216942293462621132698205097190096991916709625976826523765493530001], [78212249173117191675170269491819725722517802312978337273804090104803606178852022644248470195807846920777359458397572673319629877881485882414961268159575924654736302449378271858232975357320988498416055914130853390645176331442047110403763360174417255005631946157490069743178573263637578884793651847627029051991, 74927379501472932120680494090445315819870183792818898309591485925627415024697485507641733597293876698532213631345314279208289123258824769689285644220202046304564375857497101372953510739020984815291833079840818219941112397714761814022393125005379756778275950629416624821974542971342867918912677411141124552457, 87413688302893898473393354361135831954484558329329084401662857815823746202157926477994765338832304531581829735643758883274071789530966177809582992054303282158857862400265977801285276497220755870408421869590049299225416536929009300912398960151372766988582409763009295034261252377005456165370870094539411150067]]
hint = [[246113081383159550742301389040370789477, 0, 0], [11152329977565784221225693789680814642651917976425031602984186773217921601713987960438433946931386627886062324958107378857734386881263658081884765704688257, 10683938505657230179810827249056252019273456770047066582472908450838551957854054329645676204226277615006027375173781179496005220534722980666830108442748411, 0], [12909086249033493657373140400755388103713119422025290702729934460438874573189113819222211003617053854285976236233309899368081087581903742593207861442650517, 9187258103530841595225948803092366126509314603068288593845050883756605942036676873402194862960350885965541685057956650837894582552315218590371164516643577, 7601247345297763187625384319296811132204071832415909380474604204622868879647397909637085901563946695955258577131871160032821007989191447784910345738795389]]
'''

【解析】

问ai的历史

智谱清言.html F5刷新后立刻取消刷新来查看

解法一

看了官方WP

首先是对W进行LLL格基归约，然后把第一行做V的第一行

后面通过计算行列式得到V其他行

得到完整V后

通过W = U * V 来求U

但我并不懂为什么明明给了W，对m乘上U V 的逆矩阵就可以排除r的干扰

解法二

来源：【BaseCTF 2024】高校联合新生赛 Crypto （week1-7）_basectf新生赛-CSDN博客

构造了格 (4X6)

$\begin{bmatrix} 1&&&W_{11}&W_{12}&W_{13}\\ &1&&W_{21}&W_{22}&W_{23}\\ &&1&W_{31}&W_{32}&W_{33}\\ &&&m_{11}&m_{12}&m_{13} \end{bmatrix}$

来看看U的位数矩阵（即里面的数都是代表该位置的位数）由上三角矩阵乘下三角矩阵而得

$U= \begin{bmatrix} 512+512 & 512+512 & 512\\ 512+512 & 512+512 & 512\\ 512 & 512 & 1 \end{bmatrix}$

V的位数矩阵

$V= \begin{bmatrix} 128 & 128 & 128\\ 512 & 512 & 512 \\ 512 & 512 & 512 \end{bmatrix}$

那么W的（$W=V\cdot U$）

$W= \begin{bmatrix} 1024+512 & 1024+512 & 1024+512\\ 1024+512 & 1024+512 & 1024+512\\ 512+512 & 512+512 & 512+512 \end{bmatrix}$

mat_flag = matrix([flag1, flag2, flag3])，

m = mat_flag * W + r

r的位数矩阵

$r= \begin{bmatrix} 16 & 16 & 16 \end{bmatrix}$

那么m的矩阵抽象表示为 (1x3)

$m= \begin{bmatrix} [ flag1\cdot W_{11}+flag2\cdot W_{22}+flag3\cdot W_{33}+r_{11} & flag1\cdot W_{21}+flag2\cdot W_{22}+flag3\cdot W_{23}+r_{12} & flag1\cdot W_{31}+flag2\cdot W_{32}+flag3\cdot W_{33}+r_{13} ] \end{bmatrix}$

“””依然是Ax+e=B

这题给了个迷惑项hint,V的9个变量给了6个，不过这题拿W和m构造格的话用不着。”””

停滞一周，先留下问题吧，等我后面彻底搞懂格与格基归约是什么的时候再来解答自己的问题。

构造格是为了格基归约找到更好的基，从而在里面找到自己想要的数。

那么用什么标准来判断一个基是否比另一个基更好？

格基归约背后的原理是什么？

【EXP】

官方解

# sagemath
import numpy as np
from Crypto.Util.number import *
from re import sub

m = 
W = 
hint = 


def m2l(data):
    data = str(list(data)).replace(')',']').replace('(','[')
    return data

def red(data):
    new = sub(' +', ' ',str(data)).replace('[','').replace(']','').split(' ')
    a,b,c = new[-3:]
    a,b,c = count(a), count(b), count(c)
    return matrix([a,b,c])

def count(data):
    if '/' in data:
        a,b = data.split('/')
        a,b = int(a), int(b)
        if (a%b) >= (b//2):
            new = (a // b) + 1
        else:
            new = a // b
    else:
        new = int(data)
    return new

V = matrix(hint)
V[0] = matrix(W).LLL()[0]
V[1,2] = (abs(matrix(W).det()) - (
        V[0,0]*V[1,1]*V[2,2] +
        V[1,0]*V[2,1]*V[0,2] 
        ) + (
        V[2,0]*V[1,1]*V[0,2] +
        V[0,1]*V[1,0]*V[2,2]
        )) // (
        V[0,1]*V[2,0] - V[0,0]*V[2,1]
        )

W = matrix(W)
U = W * (V**(-1))
a = b''
new_flag = (red(matrix(m) * (V**(-1))) * (U**(-1)))[0]
a += long_to_bytes(int(new_flag[0]))
a += long_to_bytes(int(new_flag[1]))
a += long_to_bytes(int(new_flag[2]))
print(a.decode())

解法二

# sagemath
import numpy as np
from Crypto.Util.number import *
from re import sub

m = 
W = 
hint = 

M = Matrix(ZZ,4,6)
for i in range(3):
    M[i,i]=1
    for j in range(3):
        M[i,3+j]=W[i][j]
    M[3,3+i] = m[0][i]
 
L = M.LLL()
 
print(L[0])
#(-344668128972923976721080062686935352, -250147495372942220965616867735647813, -296878952575142689870517162863573117, 41189, 57853, 64237)
 
print(b''.join([long_to_bytes(-i) for i in L[0][:3]]).decode())

【flag】

1	BaseCTF{A99C2980-9F32-5BDC-26E9-C0551E3997A8}

========================================================================================

rabin

【想法】：两次rabin

【题目】

from Crypto.Util.number import *


flag=b"BaseCTF{}"
m = bytes_to_long(flag)

p = getPrime(512)
q = getPrime(512)
assert p%4==3 and q%4==3
n = p*q
e = 4

c = pow(m,e,n)
print("p=",p)
print("q=",q)
print("n=",n)
print("c=",c)
print("e=",e)
"""
p= 8531212975719216550108614256955774722172741885676113601617182716356239301381951899737237219659253655889636684200345109462928796329670321336864298557778843
q= 7443256287912111739335729314443559886458007838130371799255078565502662459436043455787869631999073617967343884377537828940738213460508765519478956421282871
n= 63500004625039456439237191267891267558404574431112995926594213383621331385226487443753506088788203040258384788149958095020759745138424276657604371402824844725005596890673468964961037168078105356669148960568974603581485045691990626520286184874115519591663033533771400334558853058140717812903874350138362098253
c= 51452608438757130697131508192775727191605112918772187364577097224326062184288501602000700342623122861398852536963355962672293705131887315354242193416090384360837672258861475017098419459125395949090523474744886423754439919504732741712693909507972791203801494594878447921609420574365853676576693694677914169353
e= 4
"""

【解析】

套模板，rabin核心是二次剩余和中国剩余定理，关于rabin网上有很多师傅都写过，这里不多赘述。

【EXP】

from Crypto.Util.number import *
from gmpy2 import *

p = 8531212975719216550108614256955774722172741885676113601617182716356239301381951899737237219659253655889636684200345109462928796329670321336864298557778843
q = 7443256287912111739335729314443559886458007838130371799255078565502662459436043455787869631999073617967343884377537828940738213460508765519478956421282871
n = 63500004625039456439237191267891267558404574431112995926594213383621331385226487443753506088788203040258384788149958095020759745138424276657604371402824844725005596890673468964961037168078105356669148960568974603581485045691990626520286184874115519591663033533771400334558853058140717812903874350138362098253
c = 51452608438757130697131508192775727191605112918772187364577097224326062184288501602000700342623122861398852536963355962672293705131887315354242193416090384360837672258861475017098419459125395949090523474744886423754439919504732741712693909507972791203801494594878447921609420574365853676576693694677914169353
e = 4

def rabin(c):
    c1 = pow(c,(p+1)//4,p)
    c2 = pow(c,(q+1)//4,q)
    cp1 = p - c1
    cp2 = q - c2

    lvp = invert(p,q)
    lvq = invert(q,p)

    m1 = (p*lvp*c2 + q*lvq*c1)%n
    m2 = (p*lvp*cp2 + q*lvq*c1)%n
    m3 = (p*lvp*c2 + q*lvq*cp1)%n
    m4 = (p*lvp*cp2 + q*lvq*cp1)%n

    return m1,m2,m3,m4

M = rabin(c)

for m in M:
    for _ in rabin(m):
        if b"BaseCTF{" in long_to_bytes(_):
            print(long_to_bytes(_).decode())
            exit()

【flag】

1	BaseCTF{01c28b9c-7924-4c04-b71d-1cca15342618}

========================================================================================

哎呀数据丢失了

【想法】：读pri.pem读不出来，应该是损毁了，尝试按照格式手动修复一下

【题目】

task.py

from Crypto.Util.number import *
from gmpy2 import *
from Crypto.PublicKey import RSA

flag=b""
m=bytes_to_long(flag)

rsa=RSA.generate(1024)


c=pow(m,rsa.e,rsa.n)

with open("out",'wb') as f:
    f.write(long_to_bytes(c))

private_key=rsa.exportKey("PEM")
with open("pri.pem",'wb') as f:
    f.write(private_key)

out

1	鸇㦷뫂�ㅪ쬬︗첷㜞御ﵥ�趹쥃´䓻晞 젉Ǩ䶞낆跥뜔杢럪gﭑꐐꭹ힮횼ᇦ䥬ヘᥩㆀ付脎扝鎲鎦婟唢鵌䈴免ꜽ祖蚜獫ƾ藊죫洚㟋ᱧ

pri.pem

【解析】

参考文章：(PKCS1) RSA 公私钥 pem 文件解析 - 知乎 (zhihu.com)

ASN.1 - 维基百科，自由的百科全书 (wikipedia.org)

有意思，学了私钥证书格式，之前都是只会用Crypto库来解读证书，现在自己也能读懂一些了。

我们拿到一个损毁的私钥证书文件，打开来看能知道，星号占据了大部分地方

按照文章，讲证书里面内容出去标识头-----BEGIN RSA PRIVATE KEY-----和尾-----END RSA PRIVATE KEY-----

然后将里面内容进行 base64解码+转hex

30 82 02 5c 02 01 00 02 81 81 00 bd 27 84 84 12 2a ef 9a 69 ec 64 72 90 21 9d ed 06 ed d2 b7 61 17 21 b3 26 85 0b 2f 50 60 da ee d7 69 43 56 66 7c 47 9c a9 cc b6 96 9f 4f be 6d c7 fa 67 59 ac a2 1d 8a 96 a8 81 a8 e4 a0 21 77 32 75 7e 64 9d 50 31 91 51 1f a9 6d a4 2e d1 da 2f a3 bc 8c 9c 65 fb d9 c0 dd 6f 43 03 59 ac 45 e4 55 d3 2c 5b 0e a2 9d 21 e6 47 ff 80 e5 0a bc bb 80 f7 6a db 67 00 7a 04 e8 5d ba eb 4c 8f 1d 02 03 01 00 01 02 81 80 22 65 e3 55 59 30 71 ae 35 01 06 2b 47 46 b5 bf 7a f9 18 ce bc 5b 46 87 9b c3 aa 0b 0a a4 f2 6b 68 c4 fd b7 e2 9f 4b 2e 94 3a 64 21 f4 0a be 68 9c 6b 4f 0c 21 b6 c1 84 88 6d 50 56 f4 6c a2 69 08 54 0e c0 7b 82 ad 47 e6 67 97 1a 01 fa c6 16 2e 93 a7 fc 61 ae d5 66 0f 82 6a eb a3 4d 78 ac cd 18 fc 59 e7 92 17 01 f1 0f f5 1d 52 88 37 06 b8 64 28 7c fd b3 4e 30 9c 93 82 9d 29 d8 67 c9 02 41 00 c6 e0

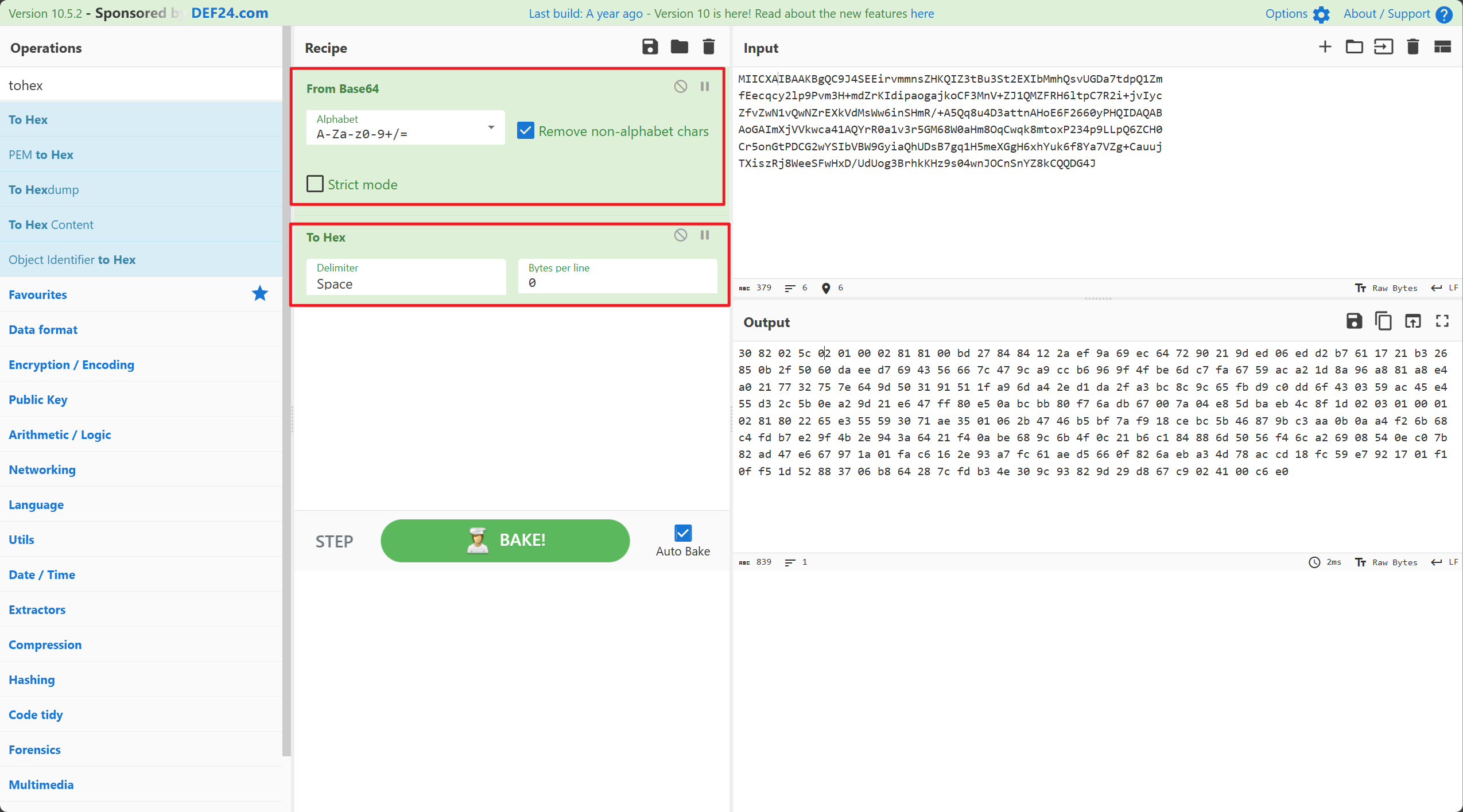
对于转出来的十六进制，解读：

02 为标识符，后面紧跟长度，长度后面就是数据内容

02就是分隔符，后面跟的是长度，长度后面是内容。

如图

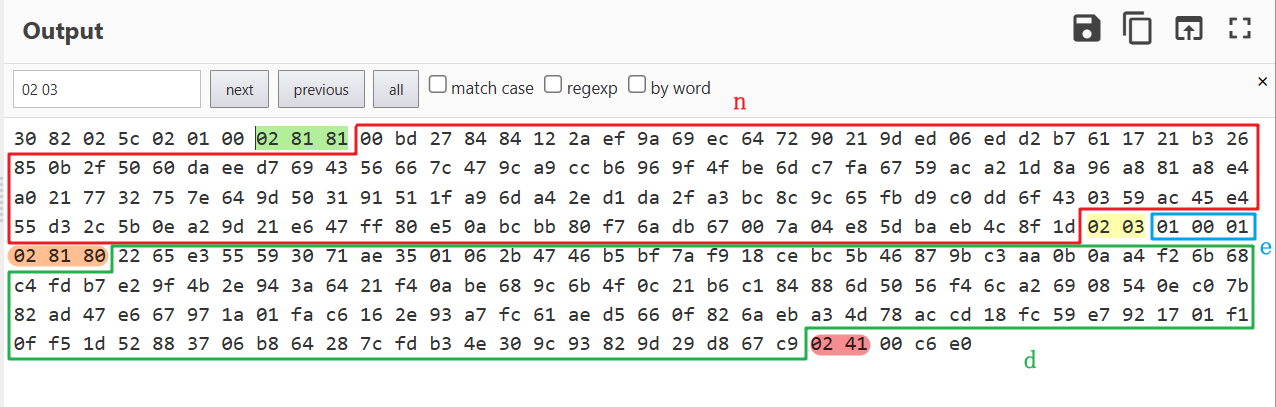
从第一行02 81 81后面开始到02 03前面都是n（十六进制表示中）
02 03 ~ 02 81 80：e
02 81 80 ~ 02 41 ：d
02 41 ~ 02 41：p
02 41 ~ 02 40：q
02 40 ~ 02 40：dp 即 $d \mod {(p-1)}$
0240 ~ 0241：dq 即 $d \mod{(q-1)}$
0241 ~ 结束：$q^{-1}\mod p$ #这个还不清楚有什么用

在这题中即使缺失了，但也关键的给出了e，n，d这三个数，其中就有解密要素n和d。

那么读十六进制给n，d就可以正常RSA解密就行了

【EXP】

from Crypto.Util.number import *

# print('00 bd 27 84 84 12 2a ef 9a 69 ec 64 72 90 21 9d ed 06 ed d2 b7 61 17 21 b3 26 85 0b 2f 50 60 da ee d7 69 43 56 66 7c 47 9c a9 cc b6 96 9f 4f be 6d c7 fa 67 59 ac a2 1d 8a 96 a8 81 a8 e4 a0 21 77 32 75 7e 64 9d 50 31 91 51 1f a9 6d a4 2e d1 da 2f a3 bc 8c 9c 65 fb d9 c0 dd 6f 43 03 59 ac 45 e4 55 d3 2c 5b 0e a2 9d 21 e6 47 ff 80 e5 0a bc bb 80 f7 6a db 67 00 7a 04 e8 5d ba eb 4c 8f 1d'.replace(" ",""))
n = 0x00bd278484122aef9a69ec647290219ded06edd2b7611721b326850b2f5060daeed7694356667c479ca9ccb6969f4fbe6dc7fa6759aca21d8a96a881a8e4a0217732757e649d503191511fa96da42ed1da2fa3bc8c9c65fbd9c0dd6f430359ac45e455d32c5b0ea29d21e647ff80e50abcbb80f76adb67007a04e85dbaeb4c8f1d

# print('22 65 e3 55 59 30 71 ae 35 01 06 2b 47 46 b5 bf 7a f9 18 ce bc 5b 46 87 9b c3 aa 0b 0a a4 f2 6b 68 c4 fd b7 e2 9f 4b 2e 94 3a 64 21 f4 0a be 68 9c 6b 4f 0c 21 b6 c1 84 88 6d 50 56 f4 6c a2 69 08 54 0e c0 7b 82 ad 47 e6 67 97 1a 01 fa c6 16 2e 93 a7 fc 61 ae d5 66 0f 82 6a eb a3 4d 78 ac cd 18 fc 59 e7 92 17 01 f1 0f f5 1d 52 88 37 06 b8 64 28 7c fd b3 4e 30 9c 93 82 9d 29 d8 67 c9'.replace(" ",""))
d = 0x2265e355593071ae3501062b4746b5bf7af918cebc5b46879bc3aa0b0aa4f26b68c4fdb7e29f4b2e943a6421f40abe689c6b4f0c21b6c184886d5056f46ca26908540ec07b82ad47e667971a01fac6162e93a7fc61aed5660f826aeba34d78accd18fc59e7921701f10ff51d52883706b864287cfdb34e309c93829d29d867c9

with open("out", "rb") as f:
    c = bytes_to_long(f.read())
m = pow(c, d, n)
print(long_to_bytes(m).decode())

【flag】

1	BaseCTF{57e6c35a-2768-49f9-8aca-47a3abcff1c7}

或许可以写一个自动点的脚本，自动根据关键词识别

详细

将关键词（02 81 81等等）放在一个数组a[]中，

读取私钥文件，去头和尾

然后调用a[]识别，然后赋值给对应的元素

（默认给e，n，d，p，q等等赋个初始值-1）

========================================================================================

Fin

PDP

【想法】：我去里面有RSA签名，AES， sha256，我的目标好像是找这玩意b'BaseCTF{' + flag_md5.hexdigest().encode() + b'}' 那么看看有什么困难。人还挺好，给了一个链接作为hint，等等，怎么是个论文？？

【题目】

from Crypto.Util.number import *
from gmpy2 import *
import hashlib
import hmac
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from random import *

def KeyGen():
    while True:
        pp=getPrime(512)
        p=2*pp+1
        while not isPrime(p):
            pp=getPrime(512)
            p=2*pp+1

        qq=getPrime(512)
        q=2*qq+1
        while not isPrime(q):
            qq=getPrime(512)
            q=2*qq+1
        
        if pp!=qq:
            break
    n=p*q
    phi=(p-1)*(q-1)

    e=getPrime(1024)
    d=invert(e,phi)

    v=getRandomNBitInteger(128)

    g=e**2%n

    return (n,g,e,d,v)

def TagBlock(n,g,d,v):
    f=open("ABigFile",'rb')
    F=f.read()
    f.close()
    b_size=64   # 64B

    block_count=len(F)//b_size + (0 if len(F)%b_size==0 else 1)

    W=[]
    tags=[]
    for i in range(block_count):
        Wi=str(v)+str(i)
        W.append(Wi)

        block=bytes_to_long(F[i*b_size:(i+1)*b_size])

        my_md5=hashlib.md5()
        my_md5.update(Wi.encode())
        tags.append(pow((int(my_md5.hexdigest(),16)*pow(g,block,n))%n,d,n))
    return (W,tags)

def GenProof(n,g):
    c=randint(400,500)
    k1=getRandomNBitInteger(256)
    k2=getRandomNBitInteger(160)
    s=getRandomNBitInteger(16)
    return (c,k1,k2,s,pow(g,s,n))

def gen_proof(n,tags,c,k1,k2,gs,judge=0):
    f=open("ABigFile",'rb')
    F=f.read()
    f.close()
    b_size=64   # 64B

    if judge:
        listF=list(F)
        X=[]
        for i in range(len(F)//100):
            x=randint(0,len(F)-1)
            while listF[x]==0:
                x=randint(0,len(F)-1)
            X.append(x)
            listF[x]=0
        F=b''
        for i in listF:
            F+=long_to_bytes(i)

    block_count=len(F)//b_size + (0 if len(F)%b_size==0 else 1)
    T=1
    temp=0
    for j in range(c):
        my_aes=AES.new(long_to_bytes(k1),mode=AES.MODE_ECB)
        i=my_aes.encrypt(pad(long_to_bytes(j),AES.block_size))
        i=bytes_to_long(i)%block_count

        my_sha256=hashlib.sha256
        my_hmac=hmac.new(long_to_bytes(k2),digestmod=my_sha256)
        my_hmac.update(long_to_bytes(j))
        a=int(my_hmac.hexdigest(),16)%n

        T=(T*(pow(tags[i],a,n)))%n

        block=bytes_to_long(F[i*b_size:(i+1)*b_size])%n

        temp=temp+block*a
    temp=pow(gs,temp,n)
    my_sha1=hashlib.sha1()
    my_sha1.update(str(temp).encode())
    rho=int(my_sha1.hexdigest(),16)
    return (T,rho)



n,g,e,d,v=KeyGen()
with open("./output/key.txt",'w') as file:
    file.write(str(n)+'\n')
    file.write(str(e)+'\n')

W,tags=TagBlock(n,g,d,v)
with open("./output/W.txt","w") as file:
    for i in W:
        file.write(str(i))
        file.write('\n')


c,k1,k2,s,gs=GenProof(n,g)
with open("./output/chal.txt",'w') as file:
    file.write(str(c)+'\n')
    file.write(str(k1)+'\n')
    file.write(str(k2)+'\n')
    file.write(str(s)+'\n')



T,rho=gen_proof(n,tags,c,k1,k2,gs)
with open("./output/result.txt",'w') as file:
        file.write(str(T)+'\n')

flag_md5=hashlib.md5()
flag_md5.update(str(rho).encode())
print(b'BaseCTF{'+flag_md5.hexdigest().encode()+b'}')

【解析】

论文给出了面对一个大文件时，客户端对服务端是否有其原始数据的快速校验方法。

还挺有意思的，有点像做零知识证明

详细请看：S-PDP/阅读笔记.md at main · naby1/S-PDP (github.com)

【EXP】

from Crypto.Util.number import *
from gmpy2 import *
import hashlib
import hmac
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from random import *


def CheckProff(n, e, W, c, k1, k2, s, T):
    tau = pow(T, e, n)
    block_count = len(W)
    for j in range(c):
        my_aes = AES.new(long_to_bytes(k1), mode=AES.MODE_ECB)
        i = my_aes.encrypt(pad(long_to_bytes(j), AES.block_size))
        i = bytes_to_long(i) % block_count

        my_sha256 = hashlib.sha256
        my_hmac = hmac.new(long_to_bytes(k2), digestmod=my_sha256)
        my_hmac.update(long_to_bytes(j))
        a = int(my_hmac.hexdigest(), 16) % n
        Wi = str(W[i])
        my_md5 = hashlib.md5()
        my_md5.update(Wi.encode())
        hw = pow(int(my_md5.hexdigest(), 16), a, n)
        tau = (tau * invert(hw, n)) % n
    tau = pow(tau, s, n)
    my_sha1=hashlib.sha1()
    my_sha1.update(str(tau).encode())
    tau = int(my_sha1.hexdigest(), 16)
    flag_md5 = hashlib.md5()
    flag_md5.update(str(tau).encode())
    print(b"BaseCTF{"+flag_md5.hexdigest().encode()+b"}")


with open("./output/key.txt", "r") as f:
    n = int(f.readline())
    e = int(f.readline())


W = []
with open("./output/W.txt", "r") as f:
    fl = f.readline()
    while fl:
        W.append(int(fl))
        fl = f.readline()


with open("./output/chal.txt", "r") as f:
    c = int(f.readline())
    k1 = int(f.readline())
    k2 = int(f.readline())
    s = int(f.readline())


with open("./output/result.txt", "r") as f:
    T = int(f.readline())


CheckProff(n, e, W, c, k1, k2, s, T)

【flag】

1	BaseCTF{d198bce7a2f06ed24d3b043bddbd7512}

========================================================================================

の歪来

【想法】：n是素数，然后e是偶数，与$\phi(n)$不互素，先解$m^{gcd(e,\phi(n))}$，再有限域开根号

【题目】

task.py

from Crypto.Util.number import *
from gmpy2 import *

flag=b''
assert len(flag)==28
m=bytes_to_long(flag)

n=getPrime(2048)
e=32

c=pow(m,e,n)


print("n =",n)
print("e =",e)
print("c =",c)

output.txt

flag = b'BaseCTF{}'
n = 17363249226879909675667629533972233798566313669420563155296918020175446973456428454735263489044575257132690882883587342817653451483222705760704890265900885255972067349104579938808591608382992680533327518070878297438339884996059309549300942570104747348751766711833983705979880714174709047335147739991850385244159235504375559144283494800573079055547597410783559965162216203307100248001158445665271438067670522510991047688414176659907164436539491205637933681658814267567385232097679554282863595183422504494357205180093828786415060565003183966959273253039416986816444073158723191290806413175478175738266995214965220231649
e = 32
c = 6840453756562205147103219479843999687625029691496635689045074720240615321966887831642035124198445485320265097191334720798522097422084141332044111764558336174743819347952914775206809737198058220362381349481027893609144697054465070779290329222696236671374412706789862193871687821041053566873553189148668599841084370137084893575567622972476409755187388121177923217208552049876944055745912987536390075417261016809335539362984984190264791744790640858201038207982043569204062714722892105134794280417020318408200038144689432974312283915592134911446185412636709207566063730723406969727969141426530341540330398465744403597273

【解析】

实践一下，$\gcd(e,\phi(n))$ =e，是很大的数，感觉用sagemath 有限域开根不行。

那么就用AMM算法来开根

【EXP】

# 创物者：善嵯峨
# 创物时间：2024/12/3 20:39
from Crypto.Util.number import *
from gmpy2 import *


# flag = b'BaseCTF{}'
n = 17363249226879909675667629533972233798566313669420563155296918020175446973456428454735263489044575257132690882883587342817653451483222705760704890265900885255972067349104579938808591608382992680533327518070878297438339884996059309549300942570104747348751766711833983705979880714174709047335147739991850385244159235504375559144283494800573079055547597410783559965162216203307100248001158445665271438067670522510991047688414176659907164436539491205637933681658814267567385232097679554282863595183422504494357205180093828786415060565003183966959273253039416986816444073158723191290806413175478175738266995214965220231649
e = 32
c = 6840453756562205147103219479843999687625029691496635689045074720240615321966887831642035124198445485320265097191334720798522097422084141332044111764558336174743819347952914775206809737198058220362381349481027893609144697054465070779290329222696236671374412706789862193871687821041053566873553189148668599841084370137084893575567622972476409755187388121177923217208552049876944055745912987536390075417261016809335539362984984190264791744790640858201038207982043569204062714722892105134794280417020318408200038144689432974312283915592134911446185412636709207566063730723406969727969141426530341540330398465744403597273

phi = n-1
g = gcd(e, phi)
e1 = e // g
phi0 = phi // g
print(g)

import math
import random
from Crypto.Util.number import *
from gmpy2 import *






def onemod(e, q):
    p = random.randint(1, q - 1)
    while powmod(p, (q - 1) // e, q) == 1:  # (r,s) = 1
        p = random.randint(1, q)
    return p


def AMM_rth(o, r, q):  # r|(q-1)
    assert ((q - 1) % r == 0)
    p = onemod(r, q)

    t = 0
    s = q-1
    while s % r == 0:
        s = s // r
        t += 1
    k = 1
    while (s*k+1) % r != 0:
        k += 1
    alp = (s*k+1) // r

    a = powmod(p, r**(t-1)*s, q)
    b = powmod(o, r*a-1, q)
    c = powmod(p, s, q)
    h = 1

    for i in range(1,t-1):
        d = powmod(int(b), r**(t-1-i), q)
        if d == 1:
            j = 0
        else:
            j = (-math.log(d, a)) % r
        b = (b*(c**(r*j))) % q
        h = (h*c**j) % q
        c = (c*r) % q
    result = powmod(o, alp, q)*h
    return  result

def ALL_Solution(m, q, rt, cq, e):
    mp = []
    for pr in rt:
        r = (pr*m) % q
        # assert(pow(r, e, q) == cq)
        mp.append(r)
    return mp

def calc(mp, mq, e, p, q):
    i = 1
    j = 1
    t1 = invert(q, p)
    t2 = invert(p, q)
    for mp1 in mp:
        for mq1 in mq:
            j += 1
            if j % 100000 == 0:
                print(j)
            ans = (mp1*t1*q+mq1*t2*p) % (p*q)
            if check(ans):
                return
    return

def check(m):
    try:
        a = long_to_bytes(m)
        if b'BaseCTF{' in a:  # 根据比赛情况修改
            print(a)
            return True
        else:
            return False
    except:
        return False

def ALL_ROOT2(r,q):    # use function set() and .add() ensure that the generated elements are not repeated
    li = set()
    while len(li) < r:
        p = powmod(random.randint(1,q-1), (q-1)//r, q)
        li.add(p)
    return li

cp = c % n


mp = AMM_rth(cp, e, n)  # AMM算法得到的一个解


rt1 = ALL_ROOT2(e,n)    # 得到所有的ri，即(ri*mp)^e%p = 1


amp = ALL_Solution(mp, n, rt1, cp, e)   # 得到所有的mp

for i in amp:
    if b"BaseCTF{" in long_to_bytes(i):
        print(long_to_bytes(i).decode())
        break

【flag】

1	BaseCTF{e_d0u_hu1_4_w@i_lal}

========================================================================================

猜猜看

【想法】：也是关于矩阵，问ai是给我们一个矩阵，然后我们输入一个矩阵，但关系还不清楚，再看看。

拿一个45x45的任意01填充的矩阵T，与m每个字节分开得到的1x45矩阵相乘，将结果y给我们；

我们还可以自己构造一个矩阵mat给服务器，让它拿这个mat与T相乘，将结果res返回。

那么就可以得到T，进而解密m

【题目】

from Crypto.Util.number import *
import socketserver
import numpy as np
import random
import ast
import os
flag = os.getenv('GZCTF_FLAG').encode()
class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self):
        return self._recvall()
    
    def handle(self):
        assert len(flag)==45
        self.send(b"hello.")

        m=bytes_to_long(flag)
        m=bin(m)[2:]

        length=len(m)

        x=np.array([int(i) for i in m])
        T=np.array([[random.getrandbits(1) for _ in range(length)] for __ in range(length)])

        y=np.dot(x,T)
        self.send(str(list(y)).encode())

        while True:
            user_input=ast.literal_eval(self.recv().strip().decode('utf-8'))
            if isinstance(user_input,list):
                try:
                    mat=np.array(user_input)
                    res=list(np.dot(mat,T))
                    self.send(str(res).encode())
                except:
                    self.send(b'wrong!!')
            else:
                self.send(b'wrong!')
                break
        

        self.send(b"\nConnection has been closed  =.=  ")
        self.request.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 9999
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

【解析】

自己构造mat

根据

length=len(m)
x=np.array([int(i) for i in m])
T=np.array([[random.getrandbits(1) for _ in range(length)] for __ in range(length)])
y=np.dot(x,T)

x 是一维矩阵，里面包含二进制m的信息，假设列数是a，格式是1xa

T是长宽都为a的的正交矩阵

那么$x\cdot T = y$

y就是1x$a$的一维矩阵

服务器会把y给我们

那么我们也知道了a

1
2
3

mat=np.array(user_input)
res=list(np.dot(mat,T))
self.send(str(res).encode())

我们可以构造一个

1xa且只有一位是1，其余为0的一维矩阵

就可以拿到T每层的数值

有了y和T

$x\cdot T = y\\ x = y\cdot T^{-1}$

关于为什么y在点乘的右边而不是左边，笔者暂时没有找到解答

得到x后

因为“y/T”会出现小数，还需要x = np.round(x)进行四舍五入

最后二进制转十进制转字符得flag

【EXP】

import numpy as np
from Crypto.Util.number import *
from pwn import *
from tqdm import *

p = remote('gz.imxbt.cn', 20940)

p.recvuntil(b'hello.\n')
y = eval(p.recvline().decode().strip())  # 记得要加上eval()，将str转成数字数组
print(y)
print(len(y))
length = len(y)
T = []
for i in trange(length):
    mat = [0] * i + [1] + [0] * (length - i - 1)
    p.sendline(str(mat).encode())
    # print(mat)
    res = eval(p.recvline().decode().strip())
    T.append(res)
T = np.array(T)
# print('T =', T)
x = np.dot(y, np.linalg.pinv(T))  # T_ni要在右边

print(x)
x = np.round(x)
print(x)
flag = ""
for i in x:
    if i == 1:
        flag += '1'
    else:
        flag += '0'
print(long_to_bytes(int(flag, 2)))

【flag】

1	BaseCTF{edae9bdc-e251-4b92-a493-a2addd2974fa}

========================================================================================

老涩批了

【想法】：lsb？复现平台上的题目好像是docker配置文件，附件在lspl\src中

【题目】

from Crypto.Util.number import *
import socketserver
import os
import uuid 
flag = os.getenv('GZCTF_FLAG').encode()

class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self):
        return self._recvall()

    def handle(self):
        
        p=getPrime(256)
        q=getPrime(256)
        n=p*q
        e=65537
        d=inverse(e,(p-1)*(q-1))

        text=b'BaseCTF{'+str(uuid.uuid4()).encode()+b'}'

        m1=bytes_to_long(text[:len(text)//2])
        c1=pow(m1,e,n)

        m2=bytes_to_long(text[len(text)//2:])
        c2=pow(m2,e,n)

        self.send(b'n = '+str(n).encode())
        self.send(b'e = '+str(e).encode())
        self.send(b'c1 = '+str(c1).encode())
        self.send(b'c2 = '+str(c2).encode())

        while True:
            select=self.recv().strip()
            if select==b'1':
                c=int(self.recv().decode().strip())
                m=pow(c,d,n)
                res=m&1
            elif select==b'2':
                c=int(self.recv().decode().strip())
                m=pow(c,d,n)
                res=long_to_bytes(m,64)[0]
            elif select==b'3':
                user_text=self.recv().strip()
                if user_text==text:
                    self.send(flag)
                    break
                else:
                    self.send(b'try again')
                    break
            else :
                self.send(b'wrong')
                break
            self.send(str(res).encode())
        self.send(b"\nConnection has been closed  =.=  ")
        self.request.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 9999
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

【解析】

参考：RSA#Parity-Oracle-Attack | Lazzaro (lazzzaro.github.io)

3个模式

而模式一是我们来操作LSB Oracle Attack（Least Significant Bit Oracle Attack ）的地方。

不断地 c1乘上$2^e$，发送，看返回值，假设这次是i

如果是b'0'，那么$m<\frac{n}{2^i}$，即上限R是原来上限+下限的一半
如果是b'1'，那么$2^i\cdot m>n$，即下限L是原来上限+下限的一半

通过这个攻击方式，我们可以拿到一个被约束的整数

因为二分法，并且在这题中所有参数都在整数域中，那么经过有限次二分法后就必定能找到一个整数m

而模式二是MSB Oracle Attack（Most Significant Bit Oracle Attack ）

不断发送$c2\cdot {2^e}^i$，看返回值,如果它返回的不是预定的填充头\x00，那么就有$m2\cdot 2^i>2^{kbit}$

由二分法得，此时$m2\cdot \frac{2^i}{2}<2^{kbit}$

有了上限和下限，那么找x，$x = \frac{L+R}{2}$

关于EXP中flag2flag2 = (2**(kbits-8)//L)为什么要多减一个8，因为原本还会有个\x00在末尾

【EXP】

from Crypto.Util.number import *
import decimal
from pwn import *
from time import *
from tqdm import *

rem = remote('gz.imxbt.cn', 20794)
rem.recvuntil(b'n = ')
n = int(rem.recvline().decode().strip())

rem.recvuntil(b'e = ')
e = int(rem.recvline().decode().strip())

rem.recvuntil(b'c1 = ')
c1 = int(rem.recvline().decode().strip())

rem.recvuntil(b'c2 = ')
c2 = int(rem.recvline().decode().strip())

def server_decode_one(c):
    rem.sendline(b'1')
    sleep(0.01)
    rem.sendline(str(c).encode())
    rec = rem.recvline().strip()
    return rec


kbits = n.bit_length()
decimal.getcontext().prec = kbits  # 设置精度

L = decimal.Decimal(0)   # 设置类型为Decimal
R = decimal.Decimal(int(n))

for i in trange(kbits+50):
    if L >= R: break
    c1 = (c1*pow(2, e, n)) % n
    recv = server_decode_one(c1)
    if recv == b'1':
        L = (L+R)//2
    else:
        R = (R+L)//2

print(long_to_bytes(int(R)))
print(long_to_bytes(int(L)-1))
print(long_to_bytes(int(L+1)))
flag1 = long_to_bytes(int(L))
sleep(0.01)

def server_decode_two(c):
    rem.sendline(b'2')
    sleep(0.01)
    rem.sendline(str(c).encode())
    rec = rem.recvline().strip()
    return rec

k = 1
while True:    # 先找到第一个上限
    c22 = (c2*pow(2, e*k, n)) % n
    res = server_decode_two(c22)
    res = int(res)
    if res&1:
        break
    k += 1

L = 2**(k-1)
R = 2**k

while True:
    if R-L == 1:
        break
    x = (L+R)//2
    c22 = (c2*pow(x, e, n)) % n
    res = server_decode_two(c22)
    res = int(res)
    print(res)
    if res:
        R = x
    else:
        L = x

flag2 = (2**(kbits-8)//L)    # 为什么要减八   把末尾的\x00去掉
print(long_to_bytes(flag2))
user_text = flag1[:-1]+b'-'+long_to_bytes(flag2)
print(user_text)  # 此时的flag还不是正确答案，还要给3校验给另一个flag

rem.sendline(b'3')
sleep(0.01)
rem.sendline(user_text)


rem.interactive()

【flag】

1	BaseCTF{1b639591-1ce1-462d-8afc-b1fedfc2b85f}

========================================================================================

ECB是不安全的

【想法】：没有附件，只好nc试试。有点像是对AES的oracle-attack

【题目】

没有附件，纯试

【解析】

先了解一下ECB

Crypto系列——分组密码 | NSSCTF

16个字符为一组，且ECB分组模式块之间互不影响如下

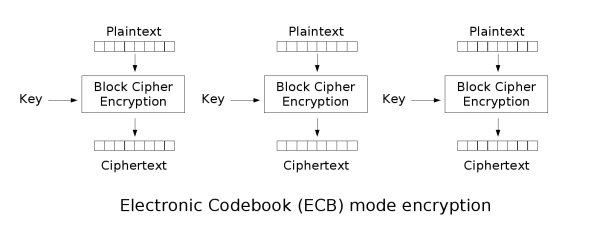
ecb_encryption

那么可以利用这个特性，填充15个任意字符’0’，让flag漏出头一位，得到此时的密文c1，

然后我们再自己在15个填充字符’0’后爆破一位i，当密文与c1相同时，那么此时爆破的i为明文（即‘B’）；

接下来填充14位’0’，让flag漏出第二位，得到此时的密文c2，

然后在14个‘0’+已知flag片段 ‘B’后爆破第二位，当密文与c1相同时，那么此时爆破的i为明文（即‘a’）；

接下来同理。

如果flag超出16位，那么在前面预留出足够空间就行（即填充31或47（16的倍数减一）……个填充字符）

用已知的flag头BaseCTF 手动爆破体现这个过程

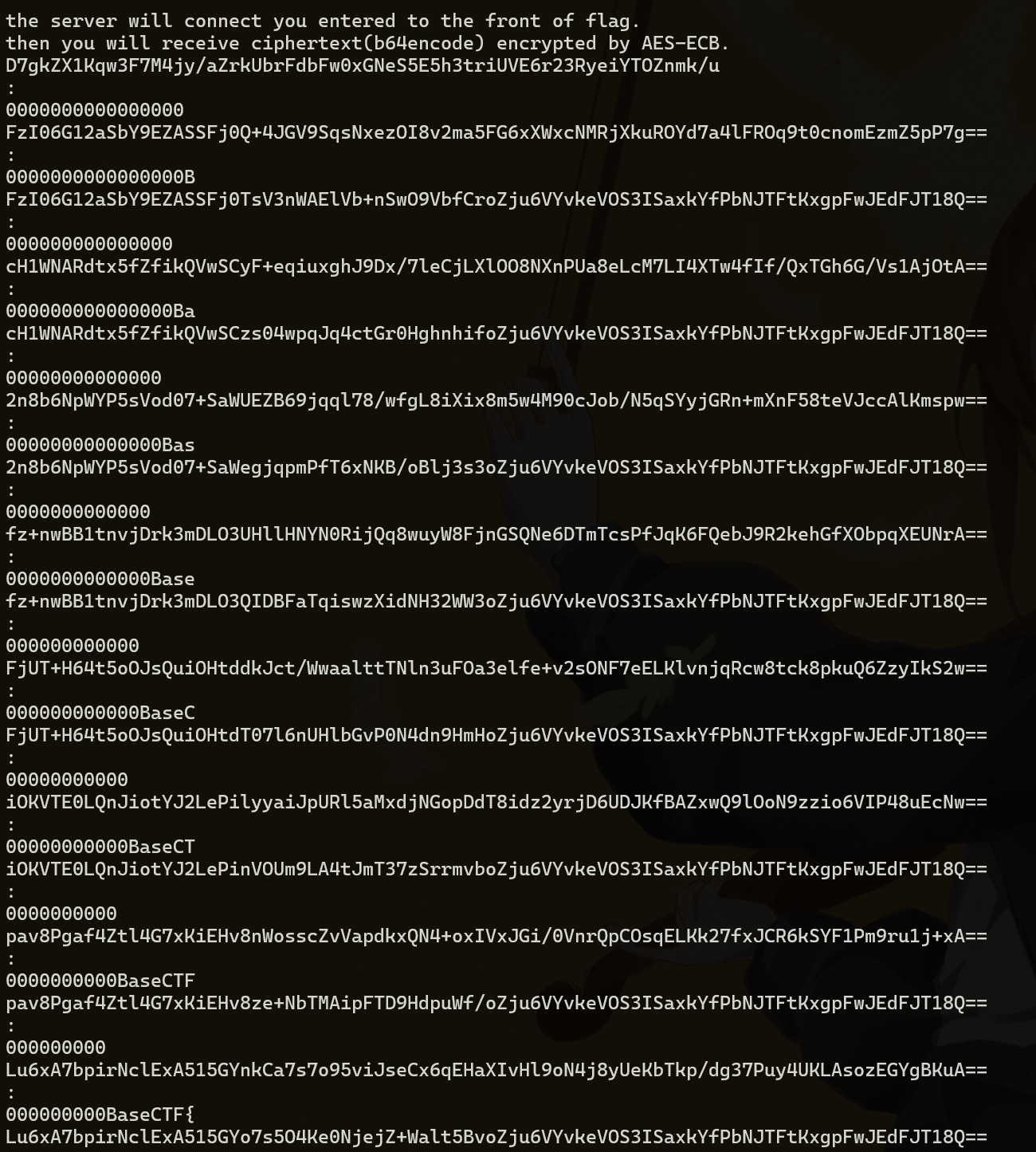
总结来说就是

步骤一：先放一位，然后得到c1

步骤二：接着自己尝试填上一个字母，补全这一块，使得加密后的密文与c1相同，加到已知flag片段中

步骤三：然后再放更多位，得到$c_i$，尝试在已知flag片段后面填上一个字母，加密得到密文与$c_i$比较，相同的明文加到已知flag片段中

重复步骤三

【EXP】

import string

from Crypto.Util.number import *
import decimal
from pwn import *
from time import *
from tqdm import *


def mysolve(m, a=1):  # m为每次发送前的提示词，a为flag索要的空间块个数，默认为1，不够可添加
    length = 16 * a

    s = b'0' * (length - 1)
    flag = ''

    for i in range(length):
        p.sendlineafter(m, s)
        res = base64.b64decode(p.recvline().decode().strip())[:(length)]  # [:length*2]  只比较前面的
        for j in range(33, 128):
            payload = '0'*((length-1)-i) + flag + chr(j)
            p.sendlineafter(m, payload)
            res2 = base64.b64decode(p.recvline().decode().strip())[:(length)]
            if res == res2:
                flag += chr(j)
                print(flag)  # 去掉末尾一个填充，放出更多flag片段
                s = s[:-1]
                break



p = remote('gz.imxbt.cn', 20856)
m = b':\n'
p.recvuntil(b'AES-ECB.\n')
print(p.recvline())

mysolve(m, 3)  # 1太小了

【flag】

1	BaseCTF{37d03b65-5c3d-45fd-9260-37496cad8cfe}

复盘结束感想

学到挺多东西的——copper，矩阵（三角矩阵，行列式，LLL运用），md5拓展长度攻击和分组密码

途中写了几篇笔记（欧几里得算法等等）

接下来搞完期末考就开始 0XGAME的复盘！