2024国城杯

2024-12-10

字数统计: 1.2k字 | 阅读时长≈ 6分

这次和队友一起拿了个贴纸:p

里面EZ_sign学到DSA（赛后才知道），自己手推了一下公式求的e，下一块的解平方和卡住了，因为是4k+2类型的，有时间复盘一下学习。

密码，misc，re附件链接: https://pan.baidu.com/s/1h6g93s58p4yiD7qSxHXNzg?pwd=2q61 提取码: 2q61
官方WP：https://kdocs.cn/l/cetcIAL8hM4F

babyRSA

题目

from secret import flag
from Crypto.Util.number import*
from gmpy2 import*

flag = b'D0g3xGC{****************}'

def gen_key(p, q):
    public_key = p*p*q
    e = public_key
    n = p*q
    phi_n = (p-1)*(q-1)
    private_key = inverse(e,phi_n)
    return public_key,private_key,e

p = getPrime(512)
q = getPrime(512)

N,d,e = gen_key(p,q)

c = gmpy2.powmod(bytes_to_long(flag),e,N)

print(N)
print(d)
print(c)

'''
n = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
c = 82363935080688828403687816407414245190197520763274791336321809938555352729292372511750720874636733170318783864904860402219217916275532026726988967173244517058861515301795651235356589935260088896862597321759820481288634232602161279508285376396160040216717452399727353343286840178630019331762024227868572613111538565515895048015318352044475799556833174329418774012639769680007774968870455333386419199820213165698948819857171366903857477182306178673924861370469175
'''

解析

看到$n=p\cdot p\cdot q$以及给了d

那么就是

变种RSA——SchmidtSamoa

原理

从加密开始

$c \equiv m^e \pmod n$

而

$d \equiv e^{-1} \mod {(p-1)*(q-1)}$

那么

$e\cdot d \equiv 1 + k\cdot (p-1)*(q-1)$

即我们解密的模数只能是$p\cdot q$

因为解密依靠拓展欧拉函数，$a^{\phi n}\equiv 1 \pmod n$

$c^{e\cdot d} \equiv c^{(p-1)\cdot (q-1)}\cdot c\equiv c \pmod {p\cdot q}$

结合这篇看：RSA的数学背景 | saga131密之作坊

此时我们只知道n和d，$n=p\cdot p\cdot q$ ，要怎么知道$p\cdot q$呢？

别忘了e = n，我们还知道e和d，那么就可以用这两个来求$p\cdot q$

也是用到拓展欧拉函数

取一个整数a（a!=1&&a>1）

有（e=n）

$a^{n\cdot d} \equiv a \pmod {p\cdot q}\\ 即a^{n\cdot d} - a = k\cdot p\cdot q$

我们还有$n=p\cdot p\cdot q$

求n与$a^{n\cdot d} - a$ 的最大公因数就可以得到$p\cdot q$

然后解密就行。

套脚本

from gmpy2 import *
from Crypto.Util.number import *

def getPQ(pub, priv):
    return gmpy2.gcd(pub, gmpy2.powmod(2, pub*priv, pub)-2)


def decrypt(pub, priv, enc):
    return gmpy2.powmod(enc, priv, getPQ(pub, priv))

n = 
d = 
c = 


pq = getPQ(n, d)
m = decrypt(n, d, c)
print(long_to_bytes(m).decode())

flag

1	D0g3xGC{W1sh_Y0u_Go0d_L@ucK-111}

Curve

还没学ecc，只好在github上找一下有无相似的题目

搜索关键代码块

1	(agx^2+gy^2)%p==(1+dgx^2*gy^2)%p

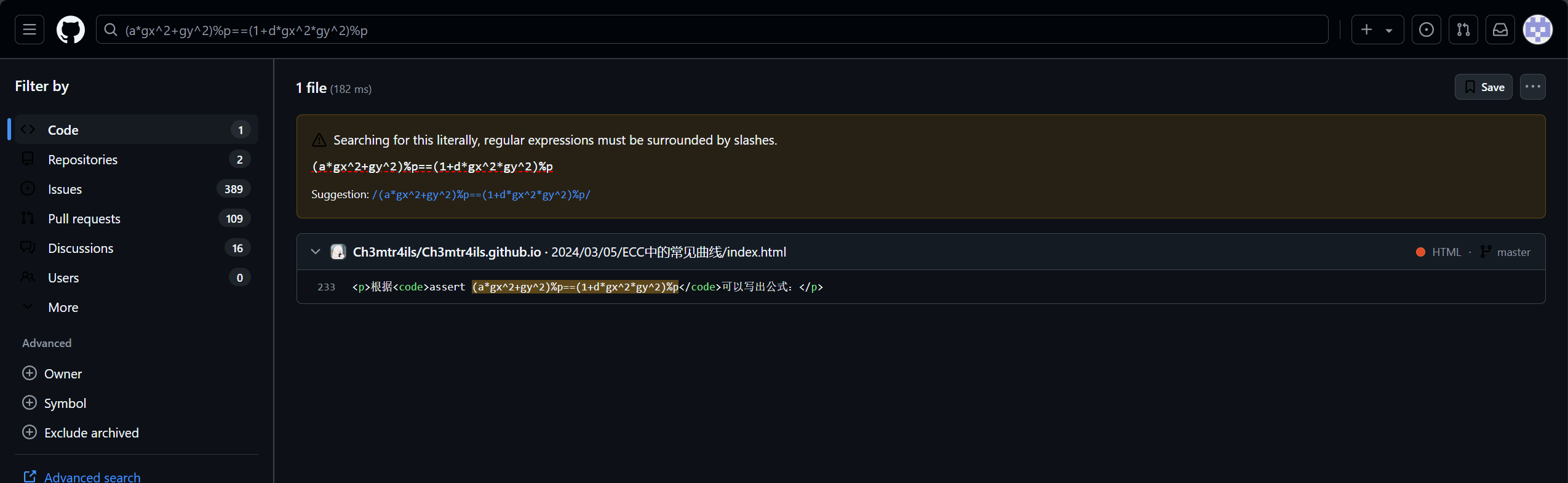
下载下来然后阅读

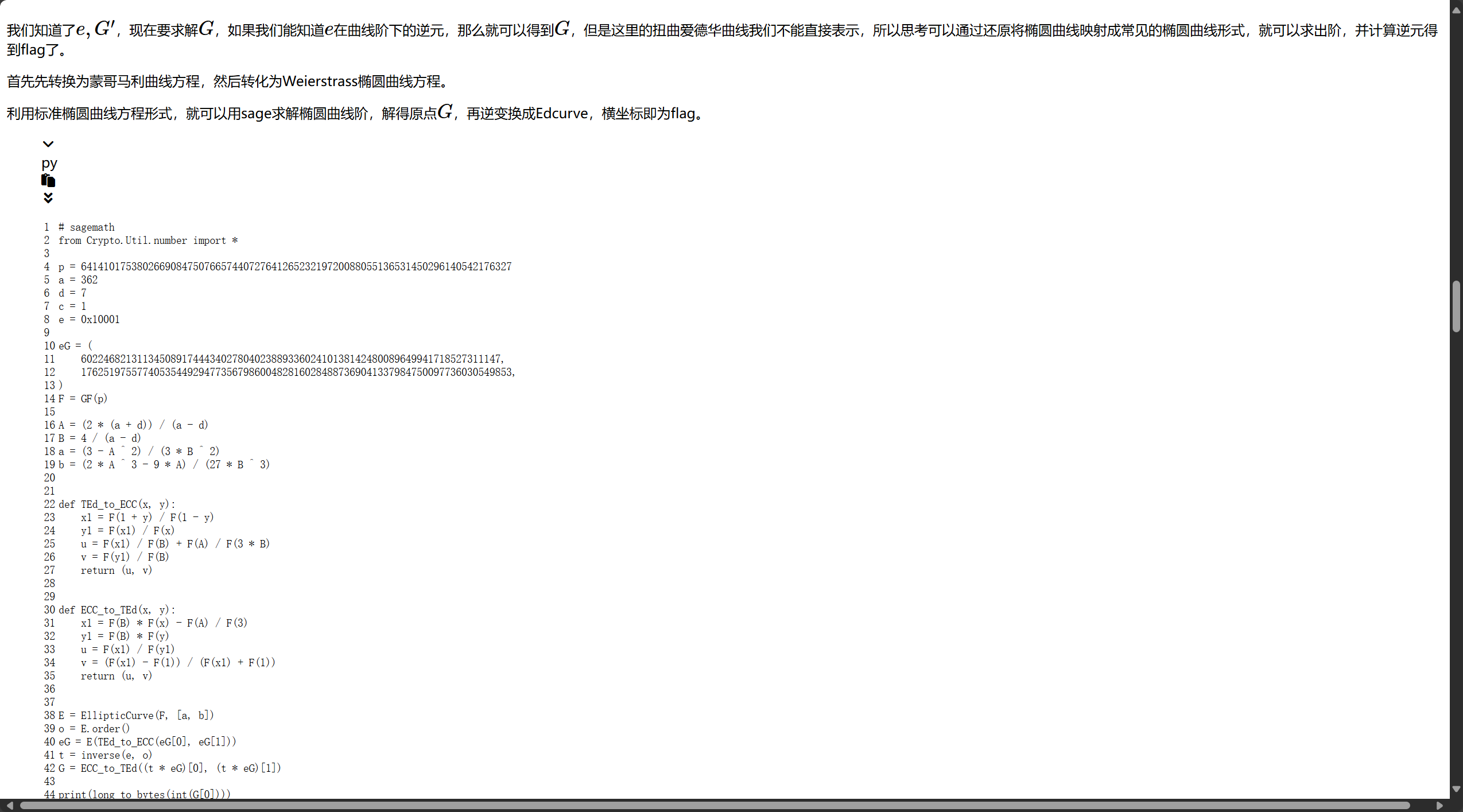
有类似的题目

套脚本

# sagemath
from Crypto.Util.number import *

p = 64141017538026690847507665744072764126523219720088055136531450296140542176327
a = 362
d = 7
c = 1
e = 0x10001

eG = 
F = GF(p)

A = (2 * (a + d)) / (a - d)
B = 4 / (a - d)
a = (3 - A ^ 2) / (3 * B ^ 2)
b = (2 * A ^ 3 - 9 * A) / (27 * B ^ 3)


def TEd_to_ECC(x, y):
    x1 = F(1 + y) / F(1 - y)
    y1 = F(x1) / F(x)
    u = F(x1) / F(B) + F(A) / F(3 * B)
    v = F(y1) / F(B)
    return (u, v)


def ECC_to_TEd(x, y):
    x1 = F(B) * F(x) - F(A) / F(3)
    y1 = F(B) * F(y)
    u = F(x1) / F(y1)
    v = (F(x1) - F(1)) / (F(x1) + F(1))
    return (u, v)


E = EllipticCurve(F, [a, b])
o = E.order()
eG = E(TEd_to_ECC(eG[0], eG[1]))
t = inverse(e, o)
G = ECC_to_TEd((t * eG)[0], (t * eG)[1])

print(long_to_bytes(int(G[0])))

1111

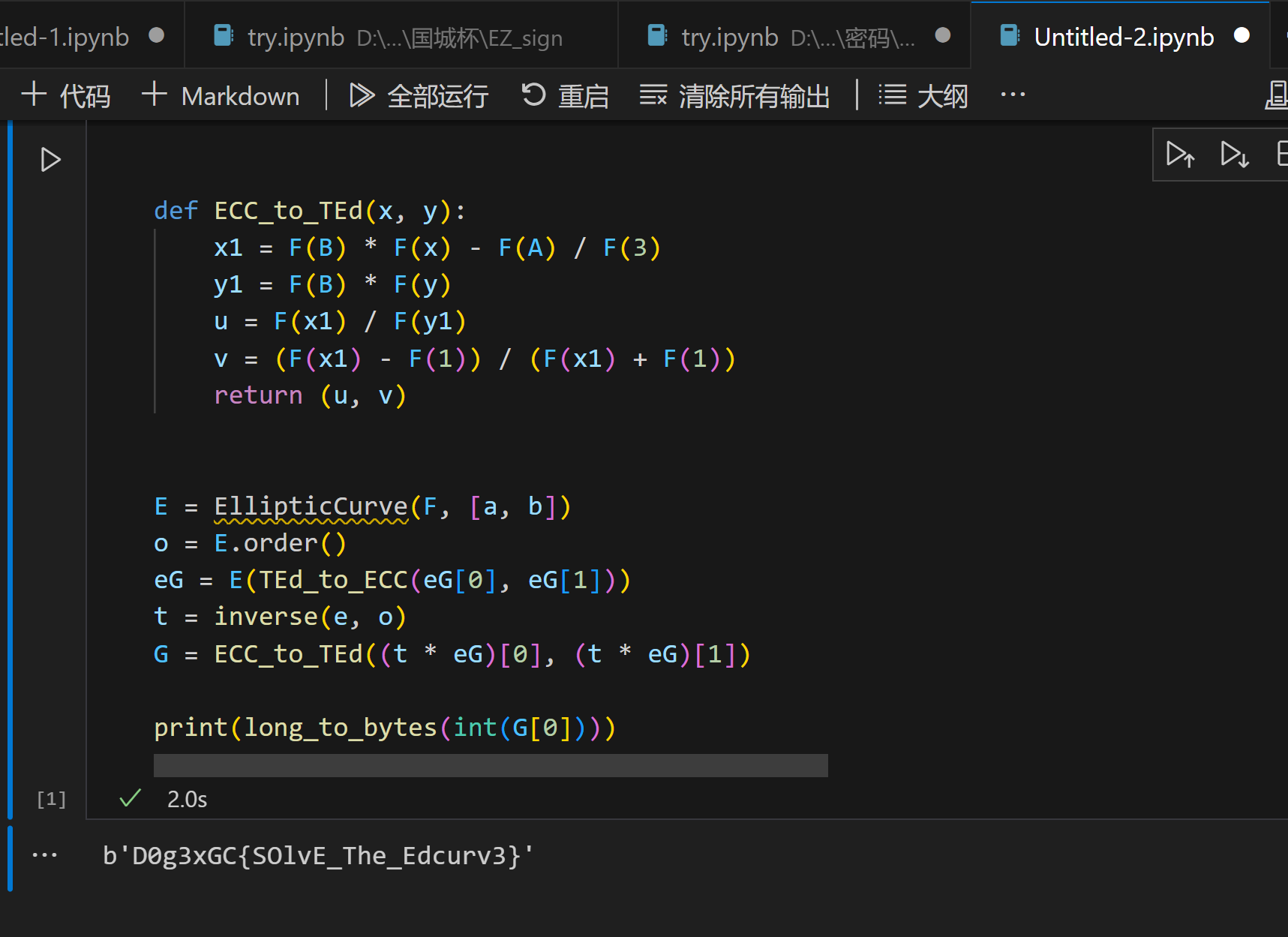
flag

1	D0g3xGC{SOlvE_The_Edcurv3}

EZ_sign

先附几张手推图片

f960bf5ba04d1f6c61da53c0d58170c

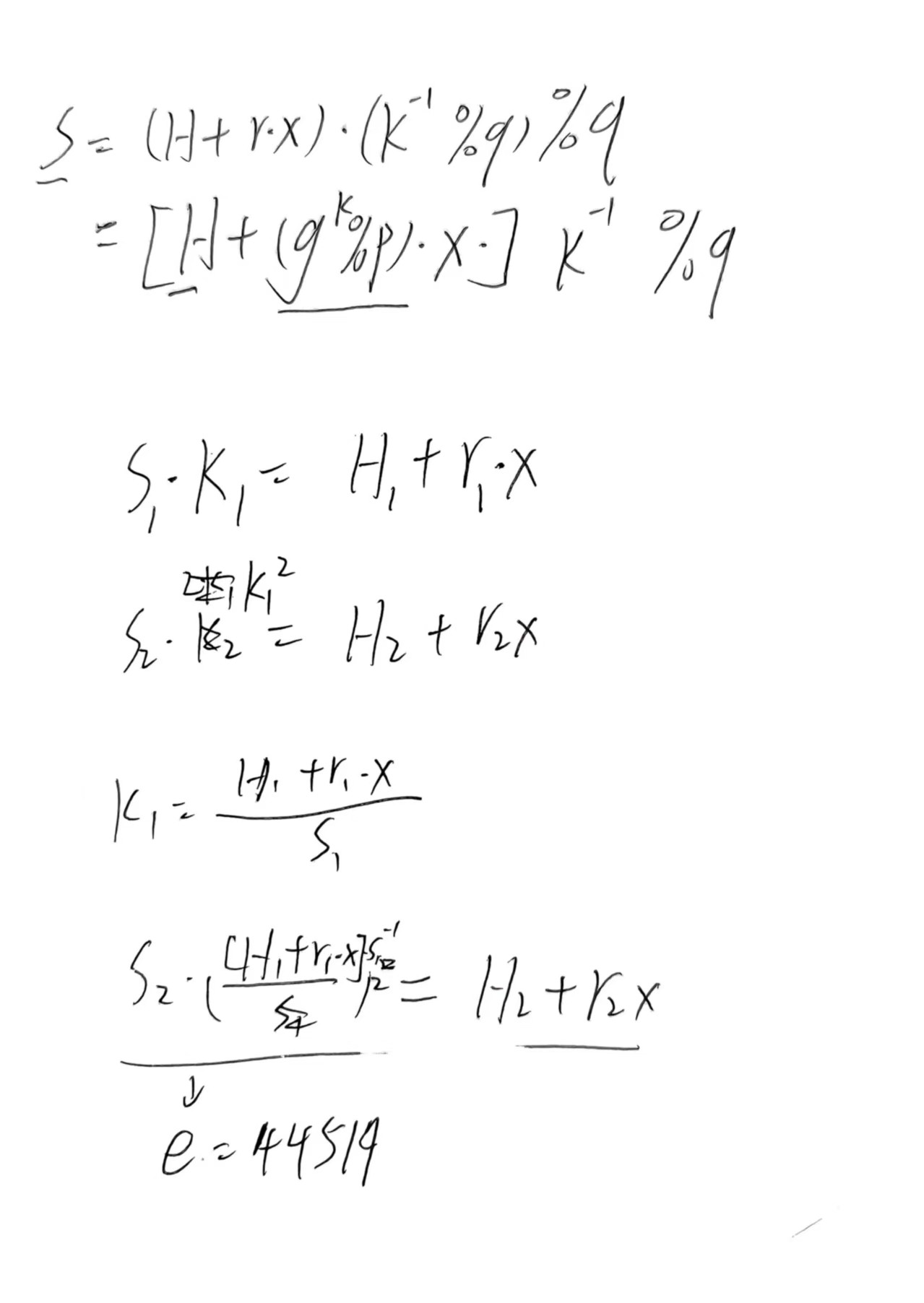
fb0c525561c46123c9b1f58f81a0ac5

关于DSA解e部分

# sagemath
from Crypto.Util.number import *
from gmpy2 import *
from tqdm import trange

a = 149328490045436942604988875802116489621328828898285420947715311349436861817490291824444921097051302371708542907256342876547658101870212721747647670430302669064864905380294108258544172347364992433926644937979367545128905469215614628012983692577094048505556341118385280805187867314256525730071844236934151633203
b = 829396411171540475587755762866203184101195238207
g = 87036604306839610565326489540582721363203007549199721259441400754982765368067012246281187432501490614633302696667034188357108387643921907247964850741525797183732941221335215366182266284004953589251764575162228404140768536534167491117433689878845912406615227673100755350290475167413701005196853054828541680397
y = 97644672217092534422903769459190836176879315123054001151977789291649564201120414036287557280431608390741595834467632108397663276781265601024889217654490419259208919898180195586714790127650244788782155032615116944102113736041131315531765220891253274685646444667344472175149252120261958868249193192444916098238

pub = (a, b, g, y)

(p, q, g, y) = pub
(H1, r1, s1) = 659787401883545685817457221852854226644541324571, 334878452864978819061930997065061937449464345411, 282119793273156214497433603026823910474682900640
(H2, r2, s2) = 156467414524100313878421798396433081456201599833, 584114556699509111695337565541829205336940360354, 827371522240921066790477048569787834877112159142
c = 18947793008364154366082991046877977562448549186943043756326365751169362247521
C = 179093209181929149953346613617854206675976823277412565868079070299728290913658

PR.<x>=PolynomialRing(GF(q))
f = H2+r2*x-s2*((H1+r1*x)*invert(s1,q))^2
f = f.monic()
res = f.roots()
# print(res)
print(long_to_bytes(int(res[1][0])))  # b'e = 44519'

后面解平方和，在用sagemath的 two_squares()求出两个合数（而p和q是素数）之后，我认为是解出了这个方程的其中一个解，而这个解明显不是我们想要的那个。

C是4k+2类型的数，网上说4k+1才有唯一解，具体看费马平方和定理

我翻了挺多文章的，找到了这个网址Integer factorization calculator (alpertron.com.ar) 不知道怎么用，也想到了用复数来分解，就是不知道怎么来求

1	C = p2+q2 = (p+qi)(p-q*i)

关于平方和分解

# sagemath
C_pq = 179093209181929149953346613617854206675976823277412565868079070299728290913658


f = ZZ[I](C_pq)
div_f = divisors(f)

for d in div_f:
    a, b = d.real(), d.imag()
    if a**2+b**2==C_pq:
        p = abs(int(a))
        q = abs(int(b))
        if is_prime(p) and is_prime(q):
            print(p,q)   # 302951519846417861008714825074296492447 295488723650623654106370451762393175957
            break

完整代码

# sagemath
from Crypto.Util.number import *
from gmpy2 import *
from tqdm import trange

a = 149328490045436942604988875802116489621328828898285420947715311349436861817490291824444921097051302371708542907256342876547658101870212721747647670430302669064864905380294108258544172347364992433926644937979367545128905469215614628012983692577094048505556341118385280805187867314256525730071844236934151633203
b = 829396411171540475587755762866203184101195238207
g = 87036604306839610565326489540582721363203007549199721259441400754982765368067012246281187432501490614633302696667034188357108387643921907247964850741525797183732941221335215366182266284004953589251764575162228404140768536534167491117433689878845912406615227673100755350290475167413701005196853054828541680397
y = 97644672217092534422903769459190836176879315123054001151977789291649564201120414036287557280431608390741595834467632108397663276781265601024889217654490419259208919898180195586714790127650244788782155032615116944102113736041131315531765220891253274685646444667344472175149252120261958868249193192444916098238

pub = (a, b, g, y)

(p, q, g, y) = pub
(H1, r1, s1) = 659787401883545685817457221852854226644541324571, 334878452864978819061930997065061937449464345411, 282119793273156214497433603026823910474682900640
(H2, r2, s2) = 156467414524100313878421798396433081456201599833, 584114556699509111695337565541829205336940360354, 827371522240921066790477048569787834877112159142
c = 18947793008364154366082991046877977562448549186943043756326365751169362247521
C_pq = 179093209181929149953346613617854206675976823277412565868079070299728290913658  # 这里是原题目的大C

PR.<x>=PolynomialRing(GF(q))
f = H2+r2*x-s2*((H1+r1*x)*invert(s1,q))^2
f = f.monic()
res = f.roots()
# print(res)
print(long_to_bytes(int(res[1][0])))

e = 44519
# print(C%4)

f = ZZ[I](C_pq)   # 一开始还以为这一块的C是代表复数，一番试探是原题目的大C，所以改名字，避免混淆
div_f = divisors(f)

for d in div_f:
    a, b = d.real(), d.imag()
    if a**2+b**2==C_pq:
        p = abs(int(a))
        q = abs(int(b))
        if is_prime(p) and is_prime(q):
            print(p,q)
            break



n = p*q

print(int(p*q).bit_length())

phi = (p-1)*(q-1)
d = int(invert(e,phi))
m = int(pow(c,d,n))
print(long_to_bytes(m).decode())

flag

1	D0g3xGC{EZ_DSA_@nd_C0mplex_QAQ}