出题记录

记录这次从9月初到10月末陆陆续续出的几道密码题

这是几次方？ 疑惑！

描述

^ w ^

^ 小猫的眼睛在python里面到底是什么意思？不如先看看大蟒蛇 运算符号的优先级吧

题目

from Crypto.Util.number import *


flag = b'flag{*****}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537

m = bytes_to_long(flag)
c = pow(m, e, n)

hint = p^e + 10086

print("c =", c)
print("[n, e] =", [n, e])
print("hint =", hint)
'''
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
[n, e] = [124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261, 65537]
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390
'''

• 出题思路

之前有遇到过运算符优先级的事，便拿来出题，异或运算符是先计算两边再进行异或的

• 解析

  结合题目描述，在网上搜索并用 AI 解读描述

  

  在 Python 中异或先计算两边，再进行异或操作

exp

from Crypto.Util.number import *
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
n, e = 124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261, 65537
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390

p = hint ^ e + 10086
q = n // p
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m).decode())

• flag

flag{yihuo_yuan_lai_xian_ji_suan_liang_bian_de2333}

欧拉欧拉！！

题目

from Crypto.Util.number import *
flag = b'flag{y0u_really_kn0w_the_phi}'
m = bytes_to_long(flag)


def get_prime(bits):
    while True:
        p = getPrime(bits)
        x = (1 << bits) - 1 ^ p
        for i in range(-10, 11):
            if isPrime(x + i):
                return p, x + i, i

p,q,i = get_prime(512)
n = p*q
e = 65537
c = pow(m, e, n)

print("c =", c)
print("n =", n)
print("i =", i)
'''
c = 14859652090105683079145454585893160422247900801288656111826569181159038438427898859238993694117308678150258749913747829849091269373672489350727536945889312021893859587868138786640133976196803958879602927438349289325983895357127086714561807181967380062187404628829595784290171905916316214021661729616120643997
n = 18104347461003907895610914021247683508445228187648940019610703551961828343286923443588324205257353157349226965840638901792059481287140055747874675375786201782262247550663098932351593199099796736521757473187142907551498526346132033381442243277945568526912391580431142769526917165011590824127172120180838162091
i = -3
'''

解析

p和q的生成方式独特，其中有

$q = x+i$

通过

x = ((1 << bits) - 1) ^ p

这行代码了解到，在二进制中p是和512个1异或得到x，

则

$p+x=2^{512} - 1$

（举例说明一下）不懂的同学可以了解一下二进制加法

a = 1001
b = a ^ 1111
b = 0110
a + b = 1111

推导得到

$p+q=2^{512} - 1+i$

phi分解

$phi = (p-1)·(q-1)=n-(p+q)+1$

带入式子得

$$phi = n - (2^{512}- 1 + i) + 1 = n - 2^{512}+2-i$$

EXP

# 创物者：善嵯峨
# 创物时间：2024/9/11 10:00
from Crypto.Util.number import *
c = 14859652090105683079145454585893160422247900801288656111826569181159038438427898859238993694117308678150258749913747829849091269373672489350727536945889312021893859587868138786640133976196803958879602927438349289325983895357127086714561807181967380062187404628829595784290171905916316214021661729616120643997
n = 18104347461003907895610914021247683508445228187648940019610703551961828343286923443588324205257353157349226965840638901792059481287140055747874675375786201782262247550663098932351593199099796736521757473187142907551498526346132033381442243277945568526912391580431142769526917165011590824127172120180838162091
i = -3
e = 65537

phi = n - 2**512 + 2 - i
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))

RSA？cmd5！

出题思路

rsa的签名，往往是给接收方B确定发送方A的身份用的，但如果发送方用不安全的哈希算法来计算信息的信息摘要，那么有可能被中途的窃密者C利用而得到明文

题目

from Crypto.Util.number import *
from gmpy2 import *
import hashlib

# 什么？你说你用md5给rsa签名了？！

m = '*******'
assert len(m) == 7
flag = 'flag{th1s_1s_my_k3y:' + m + '0x' + hashlib.sha256(m.encode()).hexdigest() + '}'

p = getStrongPrime(512)
q = getStrongPrime(512)
n = p * q
e = 65537
phi = (p - 1) * (q - 1)
d = inverse(e, phi)


def get_MD5(m0):
    import hashlib
    md5_object = hashlib.md5(m0.encode())
    md5_result = md5_object.hexdigest()
    return md5_result


def get_s(m0, d0, n0):
    hm0 = get_MD5(m0)
    hm1 = bytes_to_long(hm0.encode())
    s0 = pow(hm1, d0, n0)
    return s0


def rsa_encode(m0, e0, n0):
    m1 = bytes_to_long(m0.encode())
    c0 = pow(m1, e0, n0)
    return c0


def get_flag(m0):  # 请用这个函数来转m得到flag
    import hashlib
    flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
    print(flag)


s = get_s(m, d, n)
c = rsa_encode(flag, e, n)

print("密文c =", c)
print("签名s =", s)
print("公钥[n,e] =", [n, e])

'''
密文c = 119084320846787611587774426118526847905825678869032529318497425064970463356147909835330423466179802531093233559613714033492951177656433798856482195873924140269461792479008703758436687940228268475598134411304167494814557384094637387369282900460926092035234233538644197114822992825439656673482850515654334379332
签名s = 5461514893126669960233658468203682813465911805334274462134892270260355037191167357098405392972668890146716863374229152116784218921275571185229135409696720018765930919309887205786492284716906060670649040459662723215737124829497658722113929054827469554157634284671989682162929417551313954916635460603628116503
公钥[n,e] = [139458221347981983099030378716991183653410063401398496859351212711302933950230621243347114295539950275542983665063430931475751013491128583801570410029527087462464558398730501041018349125941967135719526654701663270142483830687281477000567117071676521061576952568958398421029292366101543468414270793284704549051, 65537]
'''

解析

这里我们得到了通过c，s，n，e，和平时的rsa不同，这里多了s，让我们看看这个s是什么

def get_MD5(m0):
    import hashlib
    md5_object = hashlib.md5(m0.encode())  # 创建MD5对象并对文本进行编码
    md5_result = md5_object.hexdigest()  # 获取加密结果
    return md5_result


def get_s(m0, d0, n0):
    hm0 = get_MD5(m0)
    hm1 = bytes_to_long(hm0.encode())
    s0 = pow(hm1, d0, n0)
    return s0

计算了m0的md5 hm0，然后将hm0转成整数hm1进行计算

$$s = hm_1^{d} \mod n$$

那么我们有e，理解rsa解密原理

$$e·d \equiv 1 \mod phi \\ s^e \equiv (hm_1^{d})^e \equiv hm_1^{d·e} \equiv hm1^{1+k·phi} \equiv hm1 \mod n = hm1$$

那么再结合题目名字和描述，去cmd5.com找hm1的结果

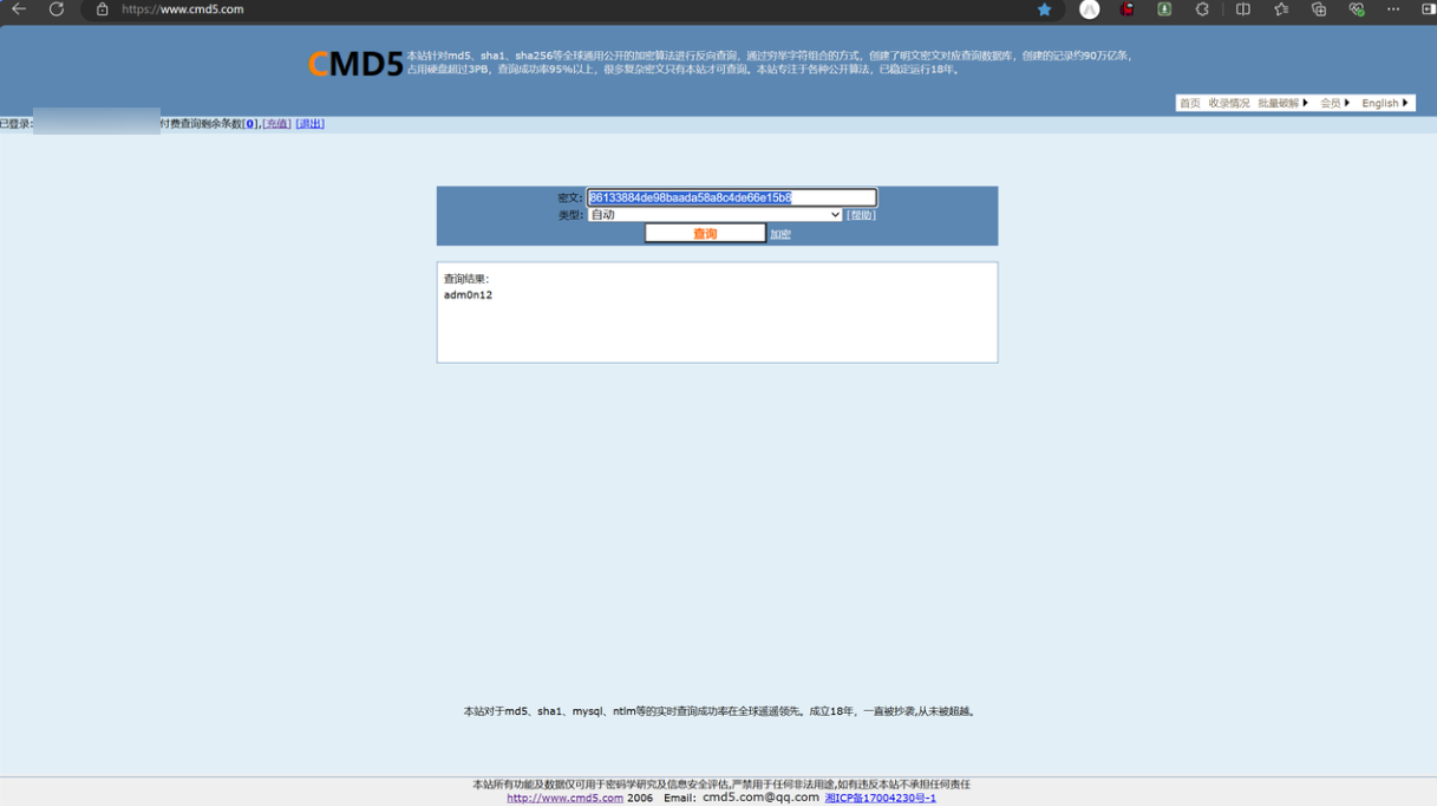
m为adm0n12

flag为

flag = 'flag{th1s_1s_my_k3y:' + m + '0x' + hashlib.sha256(m.encode()).hexdigest() + '}'

flag{th1s_1s_my_k3y:adm0n120xbfab06114aa460b85135659e359fe443f9d91950ca95cbb2cbd6f88453e2b08b}

exp

from Crypto.Util.number import *
from gmpy2 import *

s = 7270513885194445005322518350289419893608325839878215682947885852347014936106128407554345668066935779849573932055239642406851308417046145495939362638652861562381316163080735160853285303356461796079298817982074998651099375222398758502559657988024308504098238446594559605603104540325738607539729848183025647146
e = 65537
n = 118167767283404647838357773955032661171703847685597271116789633496884884504237966404005641401909577369476550625894333528860763752286157264860218284704704444830864099870199623580368198306940575628872723737071517733553706154898255520538220530675603850372384339470410704813339357637359108745206967929184573003377


def get_flag(m0):  # 请用这个函数来转m得到flag
    import hashlib
    flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
    print(flag)


hm_int = pow(s, e, n)
hm_str = long_to_bytes(hm_int).decode()
print(hm_str)  # 86133884de98baada58a8c4de66e15b8

m = 'adm0n12'  # 通过cmd5.com查询到的结果
get_flag(m)
# flag{th1s_1s_my_k3y:adm0n120xbfab06114aa460b85135659e359fe443f9d91950ca95cbb2cbd6f88453e2b08b}

格格你好棒

题目

from Crypto.Util.number import *
import random

flag = b'******'
m = bytes_to_long(flag)

a = getPrime(1024)
b = getPrime(1536)

p = getPrime(512)
q = getPrime(512)
r = random.randint(2**8, 2**9)
assert ((p+2*r) * 3*a + q) % b < 70

c = pow(m, 0x10001, p*q)

print(f'c =', c)
print(f'a =', a)
print(f'b =', b)

'''
c = 75671328500214475056134178451562126288749723392201857886683373274067151096013132141603734799638338446362190819013087028001291030248155587072037662295281180020447012070607162188511029753418358484745755426924178896079516327814868477319474776976247356213687362358286132623490797882893844885783660230132191533753
a = 99829685822966835958276444400403912618712610766908190376329921929407293564120124118477505585269077089315008380226830398574538050051718929826764449053677947419802792746249036134153510802052121734874555372027104653797402194532536147269634489642315951326590902954822775489385580372064589623985262480894316345817
b = 2384473327543107262477269141248562917518395867365960655318142892515553817531439357316940290934095375085624218120779709239118821966188906173260307431682367028597612973683887401344727494920856592020970209197406324257478251502340099862501536622889923455273016634520507179507645734423860654584092233709560055803703801064153206431244982586989154685048854436858839309457140702847482240801158808592615931654823643778920270174913454238149949865979522520566288822366419746
'''

格密码基础

格定义

https://blog.csdn.net/jayq1/article/details/140872034

矩阵乘法

https://zhuanlan.zhihu.com/p/158776486

NTRU密码

参数
模：$p$
私钥：$(f,g)$
公钥：$h=f^{−1}·g\pmod p$
临时密钥$r$

加密：

$$c≡r·h+m≡r·f^{−1}·g+m\pmod p$$

解密：

$$c≡r·g+f·m\pmod p≡f·m\pmod p(modg)$$

再乘上$f^{−1}$即可得到$m$。

参数大小：

显然当$r*g*+f*m<p,m<g$时才能正确解密。

考虑格

$$L = \begin{bmatrix} 1&h \\ 0&p\end{bmatrix}$$

同时我们有$h·f + k·p=g$，

此时我们发现 $(f,g)$便是格中的一个格点。

因为$(f,k)L=(f,f·h+p·k)=(f,g)$

则如果我们能够找到$(f,k)$ 则可以得到$(f,g)$

更多条件

$$f < \frac{1}{2}p^{\frac{1}{2}},g<\frac{1}{2}p^{\frac{1}{2}},m<\frac{1}{4}p^{\frac{1}{2}},r<\frac{1}{2}p^{\frac{1}{2}}$$

此时发现向量$\vec{b}=(f,g)$的长度为

$$||\vec{b}||=(f^2+g^2)^{\frac{1}{2}} < \frac{p}{2}$$

@分析——为什么构造这样的格

目标为$\vec{v}=(f,g)$ 私钥

已知式子

$$\begin{align*} h=f^{-1}·g\%p \rightarrow g &= h·f \%p \\ g&=\underline{h}·f + k·\underline{p} \end{align*}$$

下划线的 h和p是已知量

观察式子，左边的g是我们想要求得，右边中也有f是我们想要的，而k并不重要。

则结合向量和格

我们构造的格最后一列为 h，p或者p，h

$\vec{(f,k)}\begin{bmatrix} &&h\\&&p\end{bmatrix}$或者$\vec{(k，f)} \begin{bmatrix} &&p\\&&h\end{bmatrix}$

为了获得f，格的第一列第一个为1，然后补0 （或者相反）

$\vec{(f,k)}\begin{bmatrix} 1&h\\0&p\end{bmatrix}$或者$\vec{(k,f)} \begin{bmatrix} 0&p\\1&h\end{bmatrix}$

矩阵相乘得到结果$\vec{(f,g)}$

通过LLL算法得到最短向量$\vec{v}$

然后取值$f = \vec{v}[0] \\g=\vec{v}[1]$

又有式子

$$c = (r·h + m) \mod p$$

两边同时乘f，得

$$\begin{align*} f·c &\equiv r·h·f + m·f \mod p \\ f·c&= r·g + m·f +k·p ……式子1 \end{align*}$$

转换一下

$$m = (c-r·g·f^{-1}) \%p$$

但r未知，此路不通，回上一个式子1

在模p的同时再模上g去消r

即

$$m = (f·c \%p\%g) ·f^{-1}\%g$$

明确目标：

找到私钥（f，g）

构造格：

由公钥公式得到g = hf + kp 因为右边只有两项，确定n维数为2，且只有h和p已知，得知最后我们要构造的格的最后一列是h，p，再推出L前面相乘的向量是（f,k），最后再补上前一列1，0。

解密

用LLL算法得到最短向量v后，对照当初设想的v= （f，g），令f = v[0]，g = v[1]，

获得f，g后，带入解密式子，因为r是临时密钥，无从得知，所以我们先模上p，再模上g，消去r。最后再乘上f关于模g的逆元，求得m。

解析

从题目和描述，知识点指向 格密码

题目给了一个断言

((p+2*r) * 3*a + q) % b < 70`，可以看成`h = ((p-2·r) · 3·a + q) mod b < 70 

其中r和h都是有范围的，最大的范围r 也是2^14 - 2^15之间，对于计算机而言相当小，可以爆破，所以当成已知数

化简式子，把模消去

(p-2·r) · 3·a +k·b = h - q

和NTRU的式子相似 (NTRU: c = (r*h + m) % p)

·构造

L = [[1, 3·a],
     [0,  b ]]

发现

$(p-r,k)L = (p-2·r, -q+h)=\vec{v}$

且

$$||\vec{v}||\approx \sqrt{2}·2^{512} < \sqrt2·b^\frac{1}{2}$$

exp

#sagemath
from Crypto.Util.number import *
from tqdm import tqdm
c = 
a = 
b = 

L = Matrix(ZZ,[[1,3*a],
               [0,b]])
p,q = L.LLL()[0]    # 这里的[0]是取其中的最小向量
p,q = abs(p),abs(q)
# 爆破r和h
for r in tqdm(range(2**8,2**9)):
    for h in range(70):
        pp = p - 2*r
        qq = q + h
        phi = (pp-1)*(qq-1)
        if gcd(phi,65537) != 1:
            continue
        m = power_mod(c,inverse_mod(65537,phi),pp*qq)
        if b'flag' in long_to_bytes(m):
            print(r,h)
            print(pp,qq)
            print(long_to_bytes(m))
            print(long_to_bytes(m)==b'flag{u_are_@_master_of_latt1ce_Crypt0gr@phy}')
            exit(0)

建议升级一下sagemath版本，参照这位师傅的文章Arch下的Sage安装 - Shin’s Blog (shinichicun.top)

碎碎念

一开始听群里面说想学格密码，于是在week5打算出一个

在笔记中寻找许久，便把窃取目标盯上了xenny师傅的格密码课程的P3

直接抄违背了出题初心，但是P3的解题内核始终吸引着我，自己动手推导式子构造格，（在这对因为我窃取题目的行为而受伤的师傅们说声对不起！）

那么我就转向修改参数，以往的rsa题目，在我手动调试验证各个参数大小关系的时候，都是能满足自身的关系的。

但在这题 assert ((p-r) * a + q) % b < 50 似乎发生了变化，随意getPrime()的参数根本满足不了前面这个式子，换句话来说，这个式子太过于严谨了，怎么能取到那么合适的值，把h从1536位降到5位

答案是getPrime + 自己构造

让我们看原题目是怎么写的

a = getPrime(1024)
b = getPrime(1536)

p = getPrime(512)
q = getPrime(512)
r = random.randint(2**14, 2**15)
assert ((p-r) * a + q) % b < 50

关键步((p-r) a + q) % b < 50，那么我们只用**先getPrime()生成p，q，r，a，然后手动取一个（或者取随机数）h 就行，让b = ((p-r) a + q) - h 就行**

等想到这步时，我才发现((p-r) a + q)的位数和b相近（前者最大项是p·a），这才能使得 h = ((p-r) a + q) - b 成立，而不是 h = ((p-r) · a + q) - K·b

代码附上

a = getPrime(1024)


p = getPrime(512)
q = getPrime(512)
r = random.randint(2**8, 2**9) #这个涉及到解题的速度，我这台电脑2个/s，遍历[2**8, 2**9]要2分钟，遍历[2**14, 2**15]要2小时，速度好像也和后面构造出的格有关

print(((p+2*r) * 3*a + q).bit_length())  # 要为a的位数＋p的位数
while ((p+2*r) * 3*a + q).bit_length() != a.bit_length() + p.bit_length():
	a = getPrime(1024)
    p = getPrime(512)
    q = getPrime(512)
    r = random.randint(2**8, 2**9)

print(((p+2*r) * 3*a + q))

b = ((p+2*r) * 3*a + q) - 58   # 可改式子的系数，或者是自己搞一个式子，核心就是p*a最大，b的位数就是a的位数＋p的位数，b具体值是((p+2*r) * 3*a + q) - h ， h的值自己拟定
h = 58
print('p,q =',[p,q])
print('a,r =',[a,r])
print('b,h =',[b,h])
exit()

调试的方法

可以改a，p，q的位数，r的范围需要后面在解题代码中看看跑的速度来调整，注意：b的位数要大于2倍的p的位数（推导见Hermite定理）

式子也能改，式子的灵魂就是最大项p·a与b在位数上相近，需要自己爆破的数字很小且可控，式子的未知数个数是5个，只有2个知道范围，k和p，q都不知，式子 导向 用格级规约LLL来解决

式子各项的系数，r的可以随意改，只要不接近p//r，exp只需要改动pp = p - t*r 中的t；

a的系数改动就要改格中a的系数

q的系数改动还不太清楚，改完exp就跑不动，也许是向量内不平衡

h改动涉及爆破范围的扩大与缩小，只需要对应的改动exp的h

for h in range(50):

完整出题代码如下

from Crypto.Util.number import *
import random

flag = b''
m = bytes_to_long(flag)




if 0:
    a = getPrime(1024)


    p = getPrime(512)
    q = getPrime(512)
    r = random.randint(2**8, 2**9)

    print(((p+2*r) * 3*a + q).bit_length())  # 要为a的位数＋p的位数
    print(((p+2*r) * 3*a + q))

    b = ((p+2*r) * 3*a + q) - 58   # 可改式子的系数，或者是自己搞一个式子，核心就是p*a最大，b的位数就是a的位数＋p的位数，b具体值是((p+2*r) * 3*a + q) - h ， h的值自己拟定
    h = 58
    print('p,q =',[p,q])
    print('a,r =',[a,r])
    print('b,h =',[b,h])
    exit()

p,q =
a,r =
b,h =

assert ((p+2*r) * 3*a + q) % b < 70

c = pow(m, 0x10001, p*q)

print(f'c = {c}')
print(f'a = {a}')
print(f'b = {b}')

先将if 0 ：改为1，执行临近代码块，获取[p,q] [a,r] [b,h] 然后直接复制到下方，将if 1：改成0，获取c，a，b

提取r，复制

放到解题脚本调试

#sagemath
from Crypto.Util.number import *
from tqdm import tqdm
c = 75671328500214475056134178451562126288749723392201857886683373274067151096013132141603734799638338446362190819013087028001291030248155587072037662295281180020447012070607162188511029753418358484745755426924178896079516327814868477319474776976247356213687362358286132623490797882893844885783660230132191533753
a = 99829685822966835958276444400403912618712610766908190376329921929407293564120124118477505585269077089315008380226830398574538050051718929826764449053677947419802792746249036134153510802052121734874555372027104653797402194532536147269634489642315951326590902954822775489385580372064589623985262480894316345817
b = 2384473327543107262477269141248562917518395867365960655318142892515553817531439357316940290934095375085624218120779709239118821966188906173260307431682367028597612973683887401344727494920856592020970209197406324257478251502340099862501536622889923455273016634520507179507645734423860654584092233709560055803703801064153206431244982586989154685048854436858839309457140702847482240801158808592615931654823643778920270174913454238149949865979522520566288822366419746

L = Matrix(ZZ,[[1,3*a],
               [0,b]])
p,q = L.LLL()[0]    # 这里的[0]是取其中的最小向量
p,q = abs(p),abs(q)
# 爆破r和h
for r in tqdm(range(308,2**9)):
    for h in range(70):
        pp = p - 2*r
        qq = q + h
        phi = (pp-1)*(qq-1)
        if gcd(phi,65537) != 1:
            continue
        m = power_mod(c,inverse_mod(65537,phi),pp*qq)
        if b'flag' in long_to_bytes(m):
            print(r,h)
            print(pp,qq)
            print(long_to_bytes(m))
            print(long_to_bytes(m)==b'既定flag{}')
            exit(0)

先用r 替换

for r in tqdm(range(2**8,2**9)):

中的2**8，跳过遍历环节，看看能否得到结果

如果可以

那么再换回成2**8

看看遍历速度和所需时间，这里需要2分钟，实际上解题只需要22秒

两个sagemath版本（Windows的9.3和Linux的10.x）都要测试速度 ， 以免新生因为环境问题而困扰

更换了参数和式子，也算半个魔改了（