密码学入门指北

​ 该本为密码学入门手册，简要介绍了密码学的概念、学习密码学的意义、所需工具及学习路线。重点讲解了RSA公钥加密算法的基本原理和数学基础，并提供了Python代码实现示例。

​

密码学 入门手册

一、密码学是什么

人话：一种用来研究如何加密来保护信息，如何解密获取信息的学问。

二、为什么学密码

可以了解 开创并实现现代密码学的RSA算法、未来将抵御量子计算机的格密码等的“后量子密码技术”，以及学到在特殊情况下我们用现代计算机来破解特定的RSA现代密码和后量子密码技术的攻击手段。

密码有清晰的路线学习

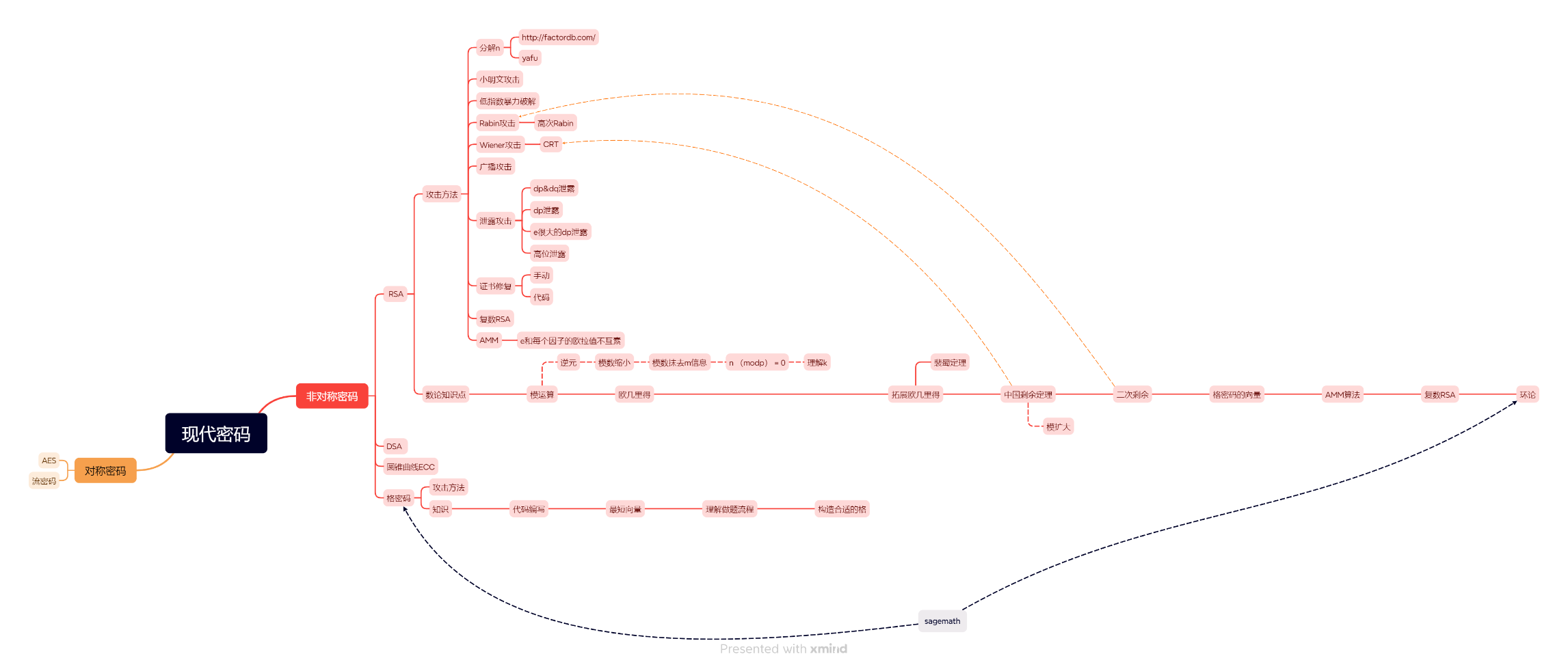
干脆的做题反馈（就跟数学题一样，会就是会，不会就是不会）

或者说没有理由，当你入门密码学的时候，就会发现做密码题也会上瘾！

三、需要的工具

1. 电脑
2. 软件：yafu，python，笔记软件
3. 草稿纸和笔（随电脑携带的，经常需要演算关系式）
4. 网站 factordb.com尝试分解n 、 探索商城 | NSSCTF 、 RSA入门 | DexterJie’Blog 等等

四、学习路线

编程：python

1. 配置好python编译器和集成开发环境（pycharm或者vscode），print("hello python world!")
2. 理解变量和变量类型，变量类型转换 a = b'65537' a = int(a)
3. 运算符号，赋值= ， 加减乘除 +-\cdot / ，整除 // ，比较大小 < > <= >= ，等于==，取模 %
4. 基本语法
5. 循环语句，布尔类型（真和假，1和0，True和False）
6. python列表，数组
7. pip install 安装pycyptodome和gmpy2包，模块导入
8. 函数的使用，pow（a,b,c） 相当于 (a ** b) % c
9. python各种进制的格式头（二进制0b，十六进制0x等等）

密码学

1. RSA公钥加密算法（推荐探索商城 | NSSCTF，挺系统的）下面我也会简单介绍RSA公钥加密算法。

数学：

1. 理解模运算
2. 逆元计算的运用（暂时不要求理解）
3. 理解海纳百川的k和无所不能的公因数

五、开始学习！

（一）掌握一定语言基础

​ 首先建议学python，密码题经常出现很大的数字和较难的运算，靠手算很难得到答案，所以需要一门计算机语言来帮我们计算。而python是符合直觉的语言，对于新手而言没有过多的条条框框，所以推荐从python入门编程语言，了解一下知识点就行。掌握下面的除画红线的知识点。

• 变量和变量类型，变量类型转换
• 运算符号
• 基本语法
• 循环语句
• 布尔类型
• 列表和元组
• 模块导入
• 函数的使用
• Python 中各种进制的格式头

讲讲我个人学习python的经历：我一开始就买了本python的入门书籍开始啃，啃到后面for循环就开始做题了，一开始也不会做题，就看别人的writeup（行话解析：看看别人的思路，抄作业，但这是个好的行为，大伙开始都是看过来的），别人的wp（writeup的缩写）一般都会有python代码，就跟着打在自己的电脑上（建议不要直接复制粘贴），遇到不会的就上网搜索，一边学密码学，一边练编程技术。

（二）了解rsa算法（公钥加密算法）

“毫不夸张地说，只要有计算机网络的地方，就有RSA算法。” ——阮一峰

1.知识点

• 元素

​ RSA算法里面一共有 8个元素。

p : 一个素数。
q : 另一个素数
n : 由p 和 q 组成的 ， 一般为 n = p x q
e : 一个被称为“公钥因子”的数。
d : 一个被称为“私钥因子”的数。下面的公式会具体展现e和d的转化。
phi : 一个与n有关，由p，q计算而得到的数。具体就是n的欧拉函数 ϕ(n) 。
m : 明文，就是要保护的信息。
c : 密文，就是要破解的信息。下面的公式会具体展现明文和密文的转化。

• 公式

​ RSA算法中一共由如下公式

​ 1.加密公式

$$c = m^{e} \pmod n$$

​ 2.解密公式

$$m = c^{d} \pmod n$$

​ 3.e和d的关系式

$$d = e^{-1} \pmod {phi}$$

​ 4.p和q是素数的情况下，n的欧拉函数phi

$$phi = (p-1)\cdot (q-1)$$

​ 5.n与p,q的关系式

$$n = p \cdot q$$

​ 6.大小关系

​

$$m < n \\ n \approx phi$$

入门后可以尝试推导一下上面的公式，入门前只需要懂得如何在python中实现上面公式即可。

• 原理

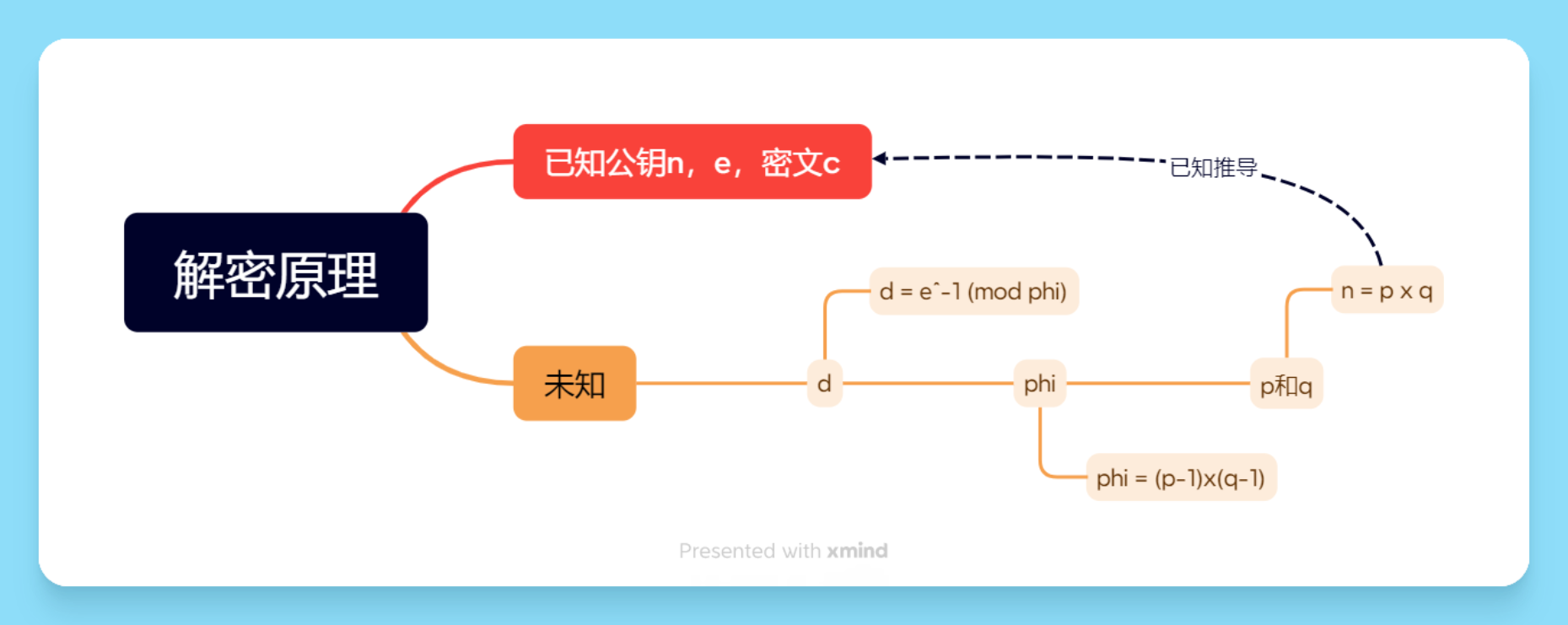
  解密原理

  一般RSA算法加密会公开公钥n和e，信息传输难免会泄露密文c，所以我们可以得到的一共有三个元素n，e，c。从上面的解密公式可以知道我们需要密钥因子d，而计算d需要e和phi，e已知，求未知的phi又需要p和q，有关p和q的式子只有一个$n=p\cdot q$

  因此解密的关键是在得到p和q

  

  难破解的原理

  RSA算法开创了现代密码并实现了非对称加密，其中难破解的原理基于大整数分解。

  计算n = p\cdot q简单，但由n分解出p，q

  手算 12 的因子，很快可以列出 [1,2,3,4,6,12]，但一旦上升到很大的整数，例如

  6969872410035233098344189258766624225446081814953480897731644163180991292913719910322241873463164232700368119465476508174863062276659958418657253738005689

  就根本拆不开成两个数字。

  我们解题的原理

  上面说到，n很难分解，那我们是靠什么来破解的呢？

  答：靠一个个特殊的情况，有时候出题人会给出泄露的d，或者p和q之间的关系让我们数学推导等等特殊情况。针对这一个个特殊情况，我们也有相应的攻击方法（如下）。

  • 小明文攻击
  • 低指数暴力破解
  • Rabin 攻击与中国剩余定理的初始应用
  • 小明文攻击
  • 广播攻击
    • 低加密指数
    • 不互素的 CRT
  • 拓展欧拉定理
  • Rabin 进阶
  • dp & dq 泄露
  • p−1 光滑
  • AMM
  • RSA 证书
    • 手动处理
    • 代码处理
  • 变种 RSA — SchmidtSamoa
  • 复数与 RSA

​

• 数学基础

  RSA中涉及到我们之前没有或者说不太重视的一些数学知识点，接下来我们一起来学习一下。

  • 取模

    ​ 上面公式四个有三个都出现了一个英文单词 mod ，这可不是游戏中打mod的意思 ， 在数学中，这被称为 “模” ，数学符号是这个%，相信大家小时候都学过余，这个就是模。12除5余2的余。接下来讲一种新的观点，12在 $\mod 5$ 的世界中就是2 ，这个世界的数学范围是[ 0 , 5 ) 。

  • 模运算

    ​ 模运算和平时的运算基本上没有太大区别，只是在模运算中，我们人为的划定了一个集合[ 0 , n ) ，其中出现的数字都不会超过这个集合。模运算也可以实现等式左右两边交换，例如e和d的关系式也可以写成 $e\cdot d = 1 \pmod n$ 。

    ​ 而运算符号加减乘除的除就有些变化了。上面的$e^{-1}$ 可以写成 $\frac {1}{e}$ ，也就是1除于e，但在模运算中不能直接除，

    例如 $\frac {a+1}{b-1} \pmod n $ 要先求b的逆元 $(b-1)^{-1}$，再将这逆元$(b-1)^{-1}$与$(a+1)$相乘。

    ​ 在上面第三个公式 e和d的关系式中有$d^{-1}$,这涉及到模运算中求逆元，这点展开会涉及到其他数学知识，这里先放着不谈。只要记住在模运算中，没有除法，只有求逆元然后再相乘。具体的代码实现会在下面讲述。

  • 海纳百川的k和无所不能的公因数

    ​ 在上面的取模和模运算中，涉及到大量的$\mod n$ ，如何转化成可以手算推理的东西呢？

    ​ 答：$k\cdot n$ 其中k是任意整数，例如 $12 \pmod 5 = 12 - 2\cdot 5$ 其中的2就是k啦。

    ​ 我们之后会遇到一部分的数学推导题，出题人会给出有关p和q的关系式。草稿纸上推理处理完关系式后，经常能得到一个有关p或者q的式子$a = b \pmod p$，此时我们只需要将这个式子转化一下 $a = b+k_1\cdot p$ 即 $k_1\cdot p = a-b$ 求 a-b 和 n 的公因数就可以得到p了，因为$n = p\cdot q$ 也可以看成 $ n = k_2\cdot p$，而$k_1$一般不等于$k_2$ 所以就可以得到p。具体情况请见羊城杯 2021Bigrsa 共享素数。

​

• 计算机基础
  • 把“我喜欢密码学”转化为整数——\cdot \cdot 编码\cdot \cdot

​ 这看起来有点不可思议，文字和数字怎么联系在一起，但计算机上就可以，计算机底层是一堆二进制，只有0和1 。要想在屏幕 上展现文字，需要”编码“，编码将数字按照规定的表转换成对应的文字，常见的编码有ASCII表。

​ 有了编码，我们就能把想保护传输的信息转换成整数，再通过RSA算法加密计算得到密文c。

$$c = m^{e} \pmod n$$

2.代码实现

• 加密脚本（不需要掌握熟背，只用知道每一行是什么意思就行）

# 导入Crypto.Util.number模块中的所有函数
from Crypto.Util.number import *
# 导入gmpy2模块，用于高性能的数学运算
import gmpy2
# 从秘密模块导入flag，通常这是CTF挑战中的隐藏信息
from 秘密 import flag

# 这是给出了flag的样式，并不是真正的flag，但已经提供了一些提示，有些题目会根据flag头来破解
flag = b"saga131{*****}"

# 生成两个256位的质数p和q
p = getPrime(256)
q = getPrime(256)

# 计算n，即p和q的乘积，用于RSA算法的模数
n = p\cdot q
# 定义公钥指数e，通常为65537
e = 65537
# 将flag转换为长整数
m = bytes_to_long(flag)

# 使用gmpy2模块的powmod函数进行模幂运算，加密消息得到密文c
c = gmpy2.powmod(m, e, n)

# 打印模数n
print(f'n = {n}')
# 打印公钥指数e
print(f'e = {e}')
# 打印加密后的密文c
print(f'c = {c}')
# 打印质数p（通常在CTF中不会直接给出）
print(f'p = {p}')
# 打印质数q（通常在CTF中不会直接给出）
print(f'q = {q}')
"""
# 以下是打印的结果，这些值通常在CTF挑战中给出
n = 4024941574680124502316363981547051098032677531528457166859670261861728313081282635664023890534034586556845494323497683923813915739234466472396261320600483
e = 65537
c = 226967182640114431119923862488626190608050511354278604627242247124377735518111678279381846350389469161980779137969837090666693533616114290831130137310320
p = 62658315832909660478685872111870233686035497063073558738980225214351386198939
q = 64236351092062515945998729497153532140067861836088195242257976217499252460697
"""

• 解密脚本（需要熟练掌握）

# 导入Crypto.Util.number模块中的所有函数，用于处理数字和字节之间的转换等
from Crypto.Util.number import *


"""输入部分"""
# 已知的模数n，用于RSA加密和解密
n = 4024941574680124502316363981547051098032677531528457166859670261861728313081282635664023890534034586556845494323497683923813915739234466472396261320600483
# 已知的公钥指数e，通常为65537
e = 65537
# 已知的密文c，需要被解密
c = 226967182640114431119923862488626190608050511354278604627242247124377735518111678279381846350389469161980779137969837090666693533616114290831130137310320
# 已知的质数p，用于计算私钥
p = 62658315832909660478685872111870233686035497063073558738980225214351386198939
# 已知的质数q，用于计算私钥
q = 64236351092062515945998729497153532140067861836088195242257976217499252460697


"""处理部分"""
# 计算欧拉函数φ(n)，用于RSA算法中的私钥计算
phi = (p-1)*(q-1)
# 计算私钥指数d，即 e在模φ(n)的逆元
d = inverse(e,phi)
# 使用私钥指数d解密密文c，得到明文m    具体就是 m = c**d (modn)
m = pow(c,d,n)
# 将解密后的长整数m转换回字符串，得到原始的flag信息
flag = long_to_bytes(m)


"""输出部分"""
# 打印解密后的flag信息
print(flag)

六、以后的路

​ 入门RSA算法后，将跟着NSSCTF的工坊课程自主继续深造RSA，在这基础上一起学习AES对称加密、圆锥曲线算法、LCG流密码、格密码和DSA密码等等。

七、写在最后的话

密码路上道阻且长，希望兄弟们能坚持下去，必定能见到密码学的彩虹！

原件

密码学入门手册.pdf